I- LỰC TỪ
1. Phương - chiều lực từ
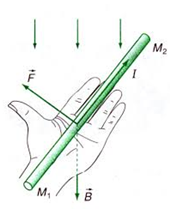
- Đặt dây dẫn \(\overline {{M_1}{M_2}} = l\) có dòng điện I chạy qua trong từ trường đều có \(\overrightarrow B \) => Xuất hiện lực từ tác dụng lên dây dẫn M1M2
- Lực từ: \(\overrightarrow F \) có:
+ Điểm đặt: Trung điểm dây M1M2
+ Phương : Vuông góc với mặt phẳng \((\overrightarrow B ,l)\)
+ Chiều: được xác định bằng quy tắc bàn tay trái
* Quy tắc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay, dòng điện chạy từ cổ tay đến ngón tay, thì ngón cái choãi ra là chiều của lực từ tác dụng lên dòng điện
2. Định luật Am-pe
Độ lớn của lực từ:
\(\begin{array}{l}F = BIl{\rm{sin}}\alpha \\\alpha {\rm{ = }}\widehat {\overrightarrow B ,l}\end{array}\)
II- BÀI TẬP XÁC ĐỊNH LỰC TỪ
Phương pháp chung
- Bước 1: Tìm các lực tác dụng lên dây dẫn có dòng điện chạy qua bao gồm
+ Ngoại lực bên ngoài tác dụng lên dây dẫn (Trọng lực, phản lực, lực masát,..)
+ Lực từ tác dụng lên dây dẫn có cường độ dòng điện chạy qua khi đặt trong từ trường đều
- Bước 2: Hợp lực tác dụng lên dây dẫn
+ Dây dẫn đứng yên: \(\sum\nolimits_{ngoailuc} {\overrightarrow F } + \overrightarrow {{F_t}} = \overrightarrow 0 {\rm{ (1)}}\)
+ Dây dẫn chuyển động biến đổi: \(\sum\nolimits_{ngoailuc} {\overrightarrow F } + \overrightarrow {{F_t}} = m\overrightarrow a {\rm{ (2)}}\)
- Bước 3: Đưa (1) hoặc (2) về phương trình đại số bằng cách:
+ Chiếu lên hệ trục tọa độ
+ Sử dụng hệ thức lượng trong tam giác vuông, tam giác thường, ...
+ \({F_{m{\rm{s}}n}} \le {\mu _n}N\)
+ \({F_{m{\rm{s}}{n_{{\rm{max}}}}}} = \mu N\)
+ Công thức liên hệ giữa khối lượng riêng trên một đơn vị chiều dài: \(m = \rho l\)
+ Công của ngoại lực: \(\begin{array}{l}{A_{ngoailuc}} = F.s.c{\rm{os}}\alpha \\\alpha = \widehat {\overrightarrow F ,s}\end{array}\)