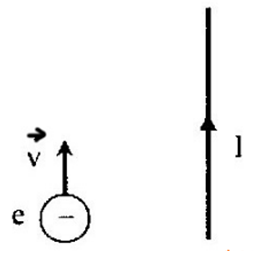
I - NHẬN XÉT
- Khi hạt điện tích q bay vào trong từ trường thì chịu tác dụng bởi trọng lực với lực lorenxơ nhưng vì \({m_q} \ll \) vì thế có thể bỏ qua trọng lực tác dụng lên điện tích
=> q chỉ chịu tác dụng bởi lực lorenxơ
- \(\overrightarrow f \bot \overrightarrow v \) => \(\overrightarrow f \) không sinh công, động năng của hạt được bảo toàn nghĩa là độ lớn vận tốc của hạt không đổi, chuyển động của hạt là chuyển động đều.
II - CHUYỂN ĐỘNG CỦA HẠT MANG ĐIỆN TRONG TỪ TRƯỜNG ĐỀU
+ Nếu \(\overrightarrow v \bot \overrightarrow B \) :
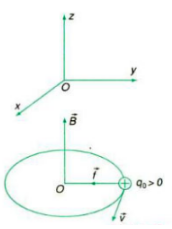
\(\left\{ \begin{array}{l}{f_{{\rm{max}}}} = \left| q \right|vB\\\overrightarrow f \bot \overrightarrow v \\f = {F_{ht}} \leftrightarrow \left| q \right|vB = m\dfrac{{{v^2}}}{R}\end{array} \right.\)
=> quỹ đạo của q là một chuyển động tròn
+ Nếu \(\overrightarrow v {\rm{//}}\overrightarrow B \):
\(\overrightarrow f = \overrightarrow 0 \) => quỹ đạo của q là một đường thẳng
=> q có chuyển động là chuyển động thẳng đều
+ Nếu \(\left( {\overrightarrow v ,\overrightarrow B } \right) = \alpha \):
=> quỹ đạo của q là một đường xoắn ốc bán kính: \(R = \dfrac{{{m_q}v\sin \alpha }}{{\left| q \right|B}}\)
III - CÁC CÔNG THỨC LIÊN QUAN
- Định lí động năng: \({A_{ngoailuc}} = \dfrac{{m{v^2}}}{2} - \dfrac{{mv_0^2}}{2} = \left| q \right|U\)
- Chu kì T(s): \(T = \dfrac{{2\pi R}}{v} = \dfrac{{2\pi }}{\omega }\) (ω: tốc độ góc (rad/s))
- Tần số f(Hz) : \(f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}\)
- Công thức liên hệ v-ω: \(v = R\omega \)
