I - MẮT THƯỜNG
- Điểm cực cận \({C_C}\) cách mắt \(25cm = O{C_C} = Đ\)
- Điểm cực viễn \({C_V}\) ở vô cùng \(O{C_V} = \infty \)
- Khoảng nhìn rõ của mắt: \(\left( {{C_C};{C_V}} \right)\)
- Công thức thấu kính mắt:
+ Độ tụ \(D = \frac{1}{f} = \frac{1}{d} + \frac{1}{{OV}}\)
+ Khi quan sát ở vô cực (không điều tiết) \(d = \infty ;D = \frac{1}{{OV}}\)
+ Khi quan sát ở cực cận (điều tiết tối đa) $d = O{C_C} = Đ;D = \frac{1}{f} = \frac{1}{Đ} + \frac{1}{{OV}}$
- Khi chuyển trạng thái quan sát vật ở vị trí cách mắt \({d_1}\) sang trạng thái quan sát vật ở vị trí cách mắt \({d_2}\) thì độ biến thiên độ tụ của mắt là: \(\Delta D = \frac{1}{{{d_2}}} - \frac{1}{{{d_1}}}\)
- Khi chuyển trạng thái từ không điều tiết sang điều tiết tối đa: \(\Delta D = \frac{1}{{O{C_C}}} - \frac{1}{{O{C_V}}}\)
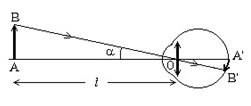
- Năng suất phân li của mắt: \(\tan \alpha = \frac{{AB}}{{OA}} = \frac{{AB}}{l}\)
II - MẮT BỊ TẬT CẬN THỊ
- Đặc điểm: ${f_{{\text{max}}}} < OV;O{C_C} < Đ = 25cm$ và \(O{C_V}\) hữu hạn
- Cách khắc phục:

III - MẮT BỊ TẬT VIỄN THỊ
- Đặc điểm: \(O{C_C} > Đ = 25cm;{f_{{\text{max}}}} > OV\)
- Cách khắc phục: Đeo kính hội tụ để nhìn gần như mắt thường tức là vật đặt cách mắt 25cm cho ảnh ảo qua kính nằm ở điểm cực cận.
\(\begin{array}{l}\left\{ \begin{array}{l}d' = - {O_k}{C_C} = - \left( {O{C_C} - L} \right)\\d = 25cm - L\end{array} \right.\\{D_k} = \frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} > 0\end{array}\)

