I- DẠNG 1: XÁC ĐỊNH CƯỜNG ĐỘ ĐIỆN TRƯỜNG TẠO BỞI ĐIỆN TÍCH ĐIỂM.
1. Áp dụng công thức định nghĩa của cường độ điện trường
\(\overrightarrow E = \dfrac{{\overrightarrow F }}{q}\)
Þ đặc điểm về phương ,chiều và độ lớn của cường độ điện trường so với \(\overrightarrow F \)
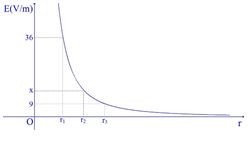
2. Cường độ điện trường tạo bởi điện tích điểm Q:
\(\overrightarrow E = k.\dfrac{Q}{{{r^2}}}.\dfrac{{\overrightarrow r }}{r}\) (*)
=> đặc điểm về phương ,chiều và độ lớn của cường độ điện trường \(\overrightarrow E \)

*Giới hạn áp dụng: (*) chỉ áp dụng được cho các trường hợp sau:
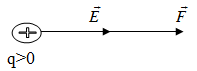
+ Điện tích điểm
+ Vật có dạng hình cầu có điện tích phân bố đều
3. Hệ quả: \(\overrightarrow F = q.\overrightarrow E \)
\( \to \left\{ \begin{array}{l}q > 0 \to \overrightarrow F \uparrow \uparrow \overrightarrow E \\q < 0 \to \overrightarrow F \uparrow \downarrow \overrightarrow E \end{array} \right.\)
II- DẠNG 2: ĐIỆN TRƯỜNG DO NHIỀU ĐIỆN TÍCH GÂY RA
- Bước 1: Xác định vị trí điểm khảo sát và tìm các điện trường thành phần xuất hiện tại điểm đó (nếu có thể thì vẽ hình)
- Bước 2: Xác định điện trường tổng hợp tại điểm khảo sát theo nguyên lí chồng chất điện trường (viết dưới dạng vec tơ)
- Bước 3: Xác định giá trị điện trường tại điểm khảo sát bằng cách biến phương trình vec tơ thành phương trình đại số
- Bước 4: Biện luận và kết luận kết quả thu được.
III- ĐIỆN TRƯỜNG BỊ TRIỆT TIÊU (CƯỜNG ĐỘ ĐIỆN TRƯỜNG TỔNG HỢP TÁC DỤNG TẠI 1 ĐIỂM BẰNG 0)
- Bước 1: Xác định vị trí điểm khảo sát và tìm các điện trường thành phần xuất hiện tại điểm đó (nếu có thể thì vẽ hình)
- Bước 2: Xác định điện trường tổng hợp tại điểm khảo sát theo nguyên lí chồng chất điện trường (viết dưới dạng vec tơ)
+ Tại vị trí mà điện trường tổng hợp tại đó bị triệt tiêu ta có:
\({\overrightarrow E _M} = {\overrightarrow E _{1M}} + {\overrightarrow E _{2M}} + ..... + {\overrightarrow E _{nM}} = \sum\limits_{i = 1}^n {\overrightarrow {{E_{iM}}} } = \overrightarrow 0 \)
+ Khi đó, lực điện tác dụng lên một điện tích diểm đặt tại đó sẽ bằng 0.
\({\overrightarrow F _M} = {\overrightarrow F _{1M}} + {\overrightarrow F _{2M}} + ..... + {\overrightarrow F _{nM}} = \sum\limits_{i = 1}^n {\overrightarrow {{F_{iM}}} }= \overrightarrow 0 \)
- Bước 3: Xác định vị trí điểm khảo sát dựa vào điều kiện suy ra từ phương trình cho điện trường tổng hợp bằng 0
- Bước 4: Gọi ẩn và tìm nghiệm đó bằng cách biến phương trình vec tơ thành phương trình đại số
- Bước 5: Biện luận và kết luận kết quả thu được