I - GIA TỐC CỦA ĐIỆN TÍCH
\(\overrightarrow a = \frac{{\overrightarrow F }}{m} = \frac{{q\overrightarrow E }}{m}\)
Độ lớn gia tốc: \(a = \frac{F}{m} = \frac{{\left| q \right|E}}{m} = \frac{{\left| q \right|U}}{{m{\rm{d}}}}\)
Trong đó:
+ \(m\): khối lượng của điện tích (kg) \({m_e} = {9,1.10^{ - 31}}kg\)
+ \(q\): điện tích (C)
+ \(U\): hiệu điện thế (V)
+ \(d\): khoảng cách giữa hai điểm dọc theo đường sức (m)
+ \(E\): cương độ điện trường (V/m)
II - CHUYỂN ĐỘNG CỦA ĐIỆN TÍCH TRONG ĐIỆN TRƯỜNG ĐỀU
1. Chuyển động của điện tích dọc theo đường sức điện trường
- \(q < 0\): chuyển động ngược chiều điện trường là chuyển động thẳng nhanh dần đều
- \(q < 0\): chuyển động cùng chiều điện trường là chuyển động thẳng chậm dần đều
- \(q > 0\): chuyển động cùng chiều điện trường là chuyển động thẳng nhanh dần đều
- \(q > 0\): chuyển động ngược chiều điện trường là chuyển động thẳng chậm dần đều.
2. Chuyển động của điện tích vuông góc với đường sức điện trường
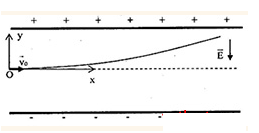
Chuyển động của điện tích được coi như chuyển động ném ngang với vận tốc ban đầu \({v_0}\)
Phương trình chuyển động: \(\left\{ \begin{array}{l}x = {v_0}t\\y = \frac{1}{2}a{t^2}\end{array} \right.\)
Phương trình quỹ đạo: \(y = \frac{{a{x^2}}}{{2v_0^2}}\)
3. Chuyển động của điện tích hợp với đường sức góc \(\alpha \)
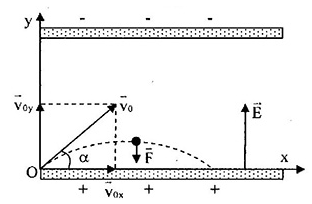
Chuyển động của điện tích được coi như chuyển động ném xiên với vận tốc \({v_0}\) hợp với phương ngang góc \(\alpha \).
Các phương trình theo các phương:
+ Vận tốc: \(\left\{ \begin{array}{l}{v_x} = {v_0}{\rm{cos}}\alpha \\{v_y} = {v_0}\sin \alpha \end{array} \right.\)
+ Chuyển động: \(\left\{ \begin{array}{l}x = \left( {{v_0}{\rm{cos}}\alpha } \right){\rm{t}}\\y = \left( {{v_0}\sin \alpha } \right)t + \frac{1}{2}a{t^2}\end{array} \right.\)
+ Quỹ đạo: \(y = \frac{{a{x^2}}}{{2{{\left( {{v_0}{\rm{cos}}\alpha } \right)}^2}}} + x\tan \alpha \)
