I - HIỆN TƯỢNG TỰ CẢM
1. Các thí nghiệm:
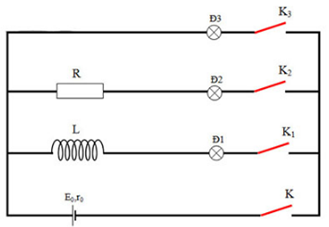
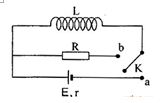
- Thí nghiệm 1: Khóa K1 và K2 đóng, K3 mở. Khí đóng khóa K, đèn 2 sáng lên ngay còn đèn 1 sáng lên chậm hơn đèn 2.
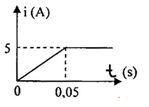
* Giải thích: Khi đóng khóa K, dòng điện qua ống dây tăng lên đột ngột trong khoảng thời gian ngắn (cường độ dòng điện tăng từ 0 - I) làm cho từ trường qua ống dây tăng lên => từ thông qua cuộn dây tăng lên
Trong khoảng thời gian từ thông qua cuộn dây biến thiên sinh ra dòng điện cảm ứng theo định luật Lenxơ, dòng điện cảm ứng có chiều chống lại sự tăng của từ thông => nó làm giảm cường độ dòng điện qua đèn 1, làm đèn 1 sáng chậm hơn đèn 2.
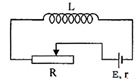
- Thí nghiệm 2: Khóa K1, K3 đóng, K2 mở. Khi ngắt khóa K, đèn 3 đang tắt bỗng sáng vụt lên rồi tắt ngay.
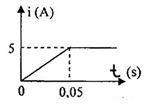
*Giải thích: Khi ngắt khóa K, dòng điện đột ngột giảm trong khoảng thời gian ngắn (cường độ từ I - 0) => từ trường qua cuộn dây L giảm => từ thông qua cuộn dây L biến thiên giảm.
Từ thông qua cuộn dây L biến thiên giảm => sinh ra dòng điện cảm ứng qua cuộn dây có chiều chống lại sự giảm => dòng điện cảm ứng này qua đèn 3 làm đèn 3 sáng vụt lên. Sau khoảng thời gian ngắt mạch không còn sự biến thiên từ thông => dòng điện cảm ứng mất đi => đèn 3 vụt tắt
2. Kết luận:
Hiện tượng tự cảm là hiện tượng cảm ứng điện từ trong một mạch điện do chính sự biến đổi của dòng điện trong mạch đó gây ra
II- SUẤT ĐIỆN ĐỘNG TỰ CẢM
1. Hệ số tự cảm
- Từ thông: \(\Phi = Li\)
Với L: hệ số tự cảm
- Hệ số tự cảm của một ống dây dài đặt trong không khí: \(L = 4\pi {.10^{ - 7}}{n^2}V = 4\pi {.10^{ - 7}}\dfrac{{{N^2}}}{l}S\)
Trong đó:
+ n: số vòng dây trên một đơn vị chiều dài của ống \((n = \dfrac{N}{l})\)
+ V: thể tích của ống \((V = lS)\)
+ S: tiết diện của ống dây (m2)
- Đơn vị của hệ số tự cảm: Henri (H)
2. Suất điện động tự cảm
Suất điện động được sinh ra do hiện tượng tự cảm gọi là suất điện động tự cảm
\({e_{tc}} = - L\dfrac{{\Delta i}}{{\Delta t}}\)
Trong đó:
+ \({e_{tc}}\): suất điện động tự cảm
+ L: hệ số tự cảm
+ ∆i: Độ biến thiên cường độ dòng điện (A)
+ ∆t: Thời gian biến thiên cường độ dòng điện (s)
+ \(\frac{{\Delta i}}{{\Delta t}}\) : tốc độ biến thiên cường độ dòng điện (A/s)
Dấu “-“ giống như công thức tính suất điện động cảm ứng theo định luật Faraday chỉ chiều dòng điện cảm ứng tuân theo định luật Lenxơ
Về mặt độ lớn, suất điện động tự cảm được tính theo biểu thức: \({e_{tc}} = L\dfrac{{\left| {\Delta i} \right|}}{{\Delta t}}\)
III- NĂNG LƯỢNG TỪ TRƯỜNG
- Năng lượng từ trường của cuộn dây:
\({\rm{W}} = \dfrac{1}{2}L{i^2}\)
Trong đó:
+ W: năng lượng từ trường của cuộn dây
+ L: hệ số tự cảm của cuộn dây (H)
+ i: Cường độ dòng điện tự cảm (A)
- Mật độ năng lượng từ trường:
\({\rm{w}} = \dfrac{1}{{8\pi }}{10^7}{B^2}\)
IV- ỨNG DỤNG CỦA HIỆN TƯỢNG TỰ CẢM
Hiện tượng tự cảm có nhiều ứng dụng trong các mạch điện xoay chiều.
Cuộn cảm là một phần tử quan trọng trong các mạch điện xoay chiều có mạch dao động và các máy biến áp.