I- CẤU TẠO LĂNG KÍNH
Định nghĩa:
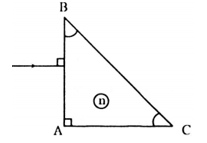
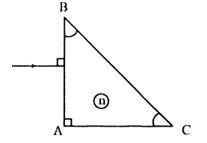
Lăng kính là một khối trong suốt, đồng nhất, được giới hạn bởi hai mặt phẳng không song song.
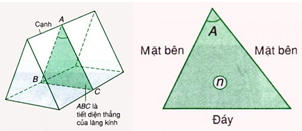
Một lăng kính được đặc trưng bởi:
- Góc chiết quang A
- Chiết suất n
II- ĐƯỜNG ĐI CỦA TIA SÁNG QUA LĂNG KÍNH
1. Tác dụng tán sắc ánh sáng trắng
Chùm ánh sáng trắng khi đi qua lăng kính sẽ bị phân tích thành nhiều chùm sáng đơn sắc khác nhau do chiết suất của chất làm lăng kính đối với mỗi ánh sáng khác nhau là khác nhau.
Đó là sự tán sắc ánh sáng.
-Trong phần này chúng ta chỉ xét ánh sáng đơn sắc.
2. Đường truyền của tia sáng qua lăng kính
Gọi n là chiết suất tỉ đối của lăng kính với môi trường chứa nó: \(n = \dfrac{{{n_{lăng \,kính}}}}{{{n_{môi \,trường}}}}\)
- Chiều lệch của tia sáng:
+ n > 1: Lệch về phía đáy lăng kính
+ n < 1: Lệch về phía đỉnh lăng kính (Trường hợp này ít gặp)
* Xét trường hợp thường gặp là n > 1:
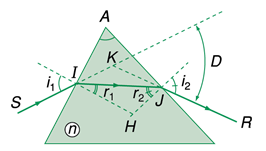
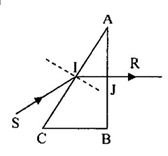
- Tia sáng ló \(JR\) qua lăng kính bị lệch về phía đáy của lăng kính so với phương của tia sáng tới.
- Vẽ đường đi của tia sáng đơn sắc qua lăng kính:
+ Khi tia sáng vuông góc với mặt lăng kính sẽ đi thẳng
+ Nếu \(r_2<i_{gh}\): tia sáng khúc xạ ra ngoài, với góc ló \(i_2\) (\(\sin {i_2} = n\sin {r_2}\))
+ Nếu \(r_2=i_{gh}=>i_2=90^0\): tia ló đi sát mặt bên thứ 2 của lăng kính
+ Nếu \(r_2>i_{gh}\): tia sáng sẽ phản xạ toàn phần tại mặt bên này ( Giả sử tại J có góc \(i’\) là góc khúc xạ và tính \(sini’ > 1\) => phản xạ toàn phần tại J)
III- CÁC CÔNG THỨC LĂNG KÍNH
- Công thức lăng kính
\(\begin{array}{l}\sin {i_1} = n\sin {r_1};{\rm{ }}\sin {i_2} = n\sin {r_2}\\{r_1} + {r_2} = A\\D = {i_1} + {i_2} - A\end{array}\)
Trong đó:
+ A: Góc chiết quang
+ D: Góc lệch
- Nếu góc chiết quang A < 100 và góc tới nhỏ, ta có:
\(\begin{array}{l}{i_1} = n{r_1};{\rm{ }}{i_2} = n{r_2}\\{r_1} + {r_2} = A\\D = A(n - 1)\end{array}\)
- Công thức tính góc lệch cực tiểu:
Khi tia sáng qua lăng kính có góc lệch cực tiểu thì đường đi của tia sáng đối xứng qua mặt phân giác của góc chiết quang của lăng kính.
Ta có:
+ \({i_1} = {i_2} = {i_m}\) (góc tới ứng với độ lệch cực tiểu)
+ \({r_1} = {r_2} = \dfrac{A}{2}\)
+ \({D_m} = 2{i_m} - A\)
+ \(\sin \dfrac{{{D_m} + A}}{2} = n\sin \dfrac{A}{2}\)
- Điều kiện để có tia ló ra cạnh bên:
+ Đối với góc chiết quang A: \(A \le 2{i_{gh}}\)
+ Đối với góc tới i: \(i \ge {i_0}\) với \(\sin {i_0} = n\sin (A - {i_{gh}})\)
IV- ỨNG DỤNG
1. Máy quang phổ
Lăng kính là bộ phận chính của máy quang phổ
Máy quang phổ phân tích ánh sáng từ nguồn phát ra thành các thành phần đơn sắc, nhờ đó xác định được cấu tạo của nguồn sáng.
2. Lăng kính phản xạ toàn phần
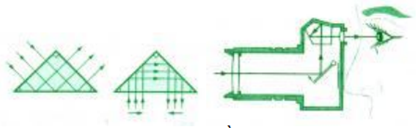
Lăng kính phản xạ toàn phần là lăng kính thủy tinh có tiết diện thẳng là một tam giác vuông cân.
Lăng kính phản xạ toàn phần được sử dụng để tạo ảnh thuận chiều (ống nhòm, máy ảnh,...)
*Chú ý:
- n là chiết suất tỉ đối của lăng kính với môi trường chứa nó: \(n = \dfrac{{{n_{lăng \,kính}}}}{{{n_{môi \,trường}}}}\)
- Do chiết suất của chất làm lăng kính là khác nhau với các ánh sáng khác nhau nên phần này chúng ta chỉ xét các tia đơn sắc tức là có một màu xác định.
- Nếu đề bài không nói lăng kính đặt trong môi trường nào thì ta hiểu lăng kính đặt trong không khí.
- Hầu hết các lăng kính đều có \(n > 1\)