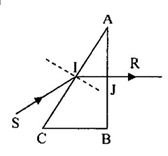
Một lăng kính có chiết suất \(n = \sqrt 2 \). Chiếu một tia sáng đơn sắc vào mặt bên của lăng kính góc tới \(i = {45^0}\), tia ló ra khỏi lăng kính vuông góc với mặt bên thứ 2 như hình vẽ. Góc chiết quang A của lăng kính:

Tỉ lệ nghịch với tiêu cự của vật kính và thị kính.

Tỉ lệ thuận với tiêu cự của vật kính và thị kính.

Tỉ lệ nghịch với tiêu cự của vật kính và tỉ lệ thuận với tiêu cự của thị kính.

Tỉ lệ thuận với tiêu cự của vật kính và tỉ lệ nghịch với tiêu cự của thị kính.

giác mạc, thủy dịch, thể thủy tinh, lòng đen (con ngươi), dịch thủy tinh, võng mạc

thủy dịch, giác mạc, thể thủy tinh, lòng đen (con ngươi), dịch thủy tinh, võng mạc

giác mạc, thủy dịch, lòng đen (con ngươi), thể thủy tinh, dịch thủy tinh, võng mạc

lòng đen (con ngươi), giác mạc, thủy dịch, võng mạc, thể thủy tinh, dịch thủy tinh

một chùm tia sáng song song với trục chính thì chùm tia ló hội tụ ở tiêu điểm ảnh sau thấu kính

Tia sáng đi qua quang tâm của thấu kính thì truyền thẳng qua thấu kính

 Một chùm tia sáng hội tụ tại tiêu điểm vật tới thấu kính thì chùm tia ló đi qua song song với trục hoành

Tia sáng đi song song với trục chính thì tia ló có đường kéo dài đi qua tiêu điểm chính của thấu kính

Vật kính là thấu kính phân kì có tiêu cự rất ngắn, thị kính là thấu kính hội tụ có tiêu cự ngắn

Vật kính là thấu kính hội tụ có tiêu cự rất ngắn, thị kính là thấu kính phân kì có tiêu cự ngắn

Vật kính là thấu kính hội tụ có tiêu cự dài, thị kính là thấu kính hội tụ có tiêu cự ngắn

Vật kính là thấu kính phân kì có tiêu cự dài, thị kính là thấu kính phân kì có tiêu cự ngắn

Lăng kính là một khối trong suốt, đồng nhất, được giới hạn bởi hai mặt phẳng song song.

 Lăng kính là một khối trong suốt, không đồng nhất, được giới hạn bởi hai mặt phẳng không song song.

Lăng kính là một khối trong suốt, đồng nhất, được giới hạn bởi hai mặt phẳng không song song.

Lăng kính là một khối đặc, đồng nhất, được giới hạn bởi hai mặt phẳng không song song.

Một khối chất trong suốt, được giới hạn bởi hai mặt cầu lồi

một khối chất trong suốt, được giới hạn bởi một mặt cầu lồi và một mặt phẳng

Một khối chất trong suốt , được giới hạn bởi 2 mặt cầu lõm

một khối chất trong suốt, được giới hạn bởi mặt cầu lồi có bán kính nhỏ hơn mặt cầu lõm

do có sự điều tiết, nên mắt có thể nhìn rõ được tất cả các vật nằm trước mắt

khi quan sát các vật dịch chuyển ra xa mắt thì thể thuỷ tinh của mắt cong dần lên

Khi quan sát các vật dịch chuyển ra xa mắt thì thể thuỷ tinh của mắt xẹp dần xuống

khi quan sát các vật dịch chuyển lại gần mắt thì thể thuỷ tinh của mắt xẹp dần xuống