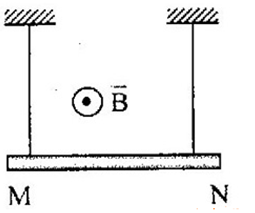
Một đoạn dây đồng \(DC\) dài \(20\,\,cm\), nặng \(12\,\,g\) được treo ở hai đầu bằng sợi dây mềm, rất nhẹ, cách điện sao cho đoạn dây \(DC\) nằm ngang. Đưa đoạn dây đồng vào trong từ trường đều có cảm ứng từ \(B = 0,2\,\,T\), hướng thẳng đứng lên trên. Dây treo có thể chịu được lực kéo lớn nhất là \(0,075\,\,N\). Lấy \(g = 10\,\,m/{s^2}\). Để dây không bị đứt thì dòng điện qua dây \(DC\) lớn nhất bằng
Trả lời bởi giáo viên
Trọng lượng của dây dẫn là:
\(P = mg = {12.10^{ - 3}}.10 = 0,12\,\,\left( N \right)\)
Giả sử dòng điện có chiều từ \(C\) đến \(D\), ta có hình vẽ:
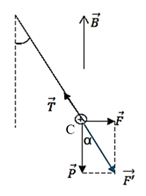
Dây dẫn nằm cân bằng, ta có:
\(\overrightarrow P + \overrightarrow F + \overrightarrow T = \overrightarrow 0 \Rightarrow \overrightarrow {F'} + \overrightarrow T = \overrightarrow 0 \Rightarrow \overrightarrow T = - \overrightarrow {F'} \Rightarrow T = F' = 2{T_C}\)
Để dây không bị đứt: \({T_C} \le 0,075\left( N \right) \Rightarrow F \le 0,15\left( N \right)\)
Từ hình vẽ ta thấy:
\(F = \sqrt {F{'^2} - {P^2}} \Rightarrow F \le \sqrt {0,{{15}^2} - 0,{{12}^2}} \Rightarrow F \le 0,09\,\,\left( N \right)\)
Lại có: \(F = IB{\rm{l}}\sin \alpha \Rightarrow I = \dfrac{F}{{B{\rm{l}}\sin \alpha }} \Rightarrow I \le \dfrac{{0,09}}{{0,2.0,2.\sin {{90}^0}}}\)
\( \Rightarrow I \le 2,25\,\,\left( A \right) \Rightarrow {I_{\max }} = 2,25\,\,\left( A \right)\)
Hướng dẫn giải:
Đoạn dây nằm cân bằng: \(\overrightarrow P + \overrightarrow T + \overrightarrow {{F_t}} = \overrightarrow 0 \)
Áp dụng quy tắc bàn tay trái
Lực từ: \({F_t} = IB{\rm{l}}\sin \alpha \)