Đề bài
Dựa vào hình 33.5, hãy thiết lập hệ thức: G∞=|k1|G2G∞=|k1|G2
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Vận dụng các công thức thấu kính
Lời giải chi tiết
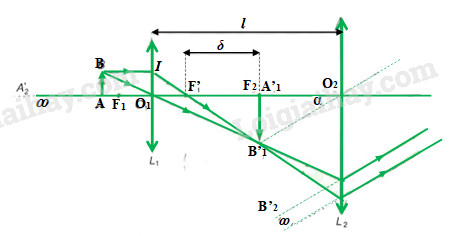
+ Ta có, độ bội giác G∞=αα0=tanαtanα0G∞=αα0=tanαtanα0 (do góc α,α0α,α0 rất nhỏ)
Từ hình, ta có: tanα0=ABOCC=ABĐ, tanα=A1′B1′O2A1′=A1′B1′f2
=> Độ bội giác: G∞=A1′B1′f2ABĐ=A1′B1′ABĐf2=|k1|G2

