Đề bài
Một tia sáng được chiếu đến điểm giữa của mặt trên một khối lập phương trong suốt, chiết suất n = 1,50 (Hình 29.6). Tính góc tới i lớn nhất để tia khúc xạ vào trong khối còn gặp mặt đáy của khối.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Công thức của định luật khúc xạ ánh sáng: n1sini = n2sinr
Lời giải chi tiết
Gọi độ dài cạnh hình lập phương là a
Theo định luật khúc xạ ánh sáng, ta có: \(1.\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}}\)
Khi \({i_{max}}\) thì \({r_{max}}\)
Ta có, \({r_{max}}\) khi tia khúc xạ đến một đỉnh ở đáy của khối lập phương.
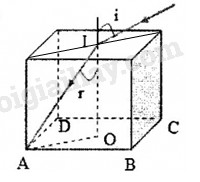
Từ hình vẽ, ta có:
\({\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{{\rm{max}}}} = \dfrac{{OA}}{{AI}} = \dfrac{{0,5{\rm{a}}\sqrt 2 }}{{\sqrt {{a^2} + {{(0,5{\rm{a}}\sqrt 2 )}^2}} }} = \dfrac{1}{{\sqrt 3 }}\)
\( \to \sin {i_{{\rm{max}}}} = n{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{{\rm{max}}}} = 1,5.\dfrac{1}{{\sqrt 3 }} \to {i_{{\rm{max}}}} = {60^0}\)

