Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
Công thức \({v^2} - v_0^2 = 2{\rm{as}}\) chỉ đúng khi chuyển động là không đổi chiều. Với v > v0 => vật chuyển động theo chiều dương, chuyển động là nhanh dần nên a và v cùng chiều do vậy a > 0, quãng đường s là một đại lượng không âm
Cho đồ thị v - t của hai ôtô như hình vẽ:
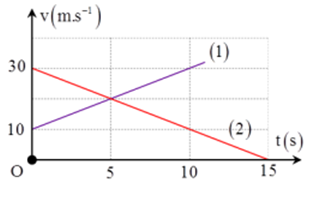
Chọn phương án đúng?
Từ đồ thị ta suy ra,
+ Phương trình vận tốc của oto 1 là: \({v_1} = 10 + 2t\)
+ phương trình vận tốc của oto 2 là: \({v_2} = 30 - 2t\)
Một vật được thả rơi tự do từ độ cao 125m xuống mặt đất. Lấy \(g = 10m/{s^2}\). Thời gian rơi của vật là
Thời gian rơi của vật là: \(t = \sqrt {\dfrac{{2h}}{g}} = \sqrt {\dfrac{{2.125}}{{10}}} = 5s\)
Phương trình chuyển động của một vật trên một đường thẳng có dạng \(x = 2{t^2} + 10t + 100(m;s)\).Thông tin nào sau đây là đúng?
Từ phương trình chuyển động ta có: \(\left\{ \begin{array}{l}{x_0} = 100m\\{v_0} = 10m/s\\a = 4m/{s^2}\end{array} \right.\)
=> Vật chuyển động nhanh dần đều với gia tốc \(a = 4{\rm{ }}m/{s^2}\)
Tọa độ lúc ban đầu của vật là \({x_0} = 100m\)
Vận tốc của vật tại thời điểm ban đầu: \({v_0} = 10m/s\)
Đồ thị tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều có dạng
Ta có phương trình tọa độ theo thời gian của chất điểm trong chuyển đông thẳng biến đổi đều có dạng: \(x = {x_0} + {v_0}t + \dfrac{1}{2}a{t^2}\)
=> Đồ thị của tọa độ theo thời gian của chất điểm chuyển động thẳng biến đổi đều là một nhánh parabol (dạng đồ thị giống hàm \(y = ax^2+bx+c\) nhưng ở đây ta có t>0 lên đồ thị chỉ là một nhánh parabol)
Đồ thị a - t của chuyển động thẳng biến đổi đều có dạng:
Đồ thị a - t của chất điểm chuyển động thẳng biến đổi đều có dạng là đường thẳng song song với trục Ot

