I. Sơ đồ tư duy Vectơ trong mặt phẳng tọa độ
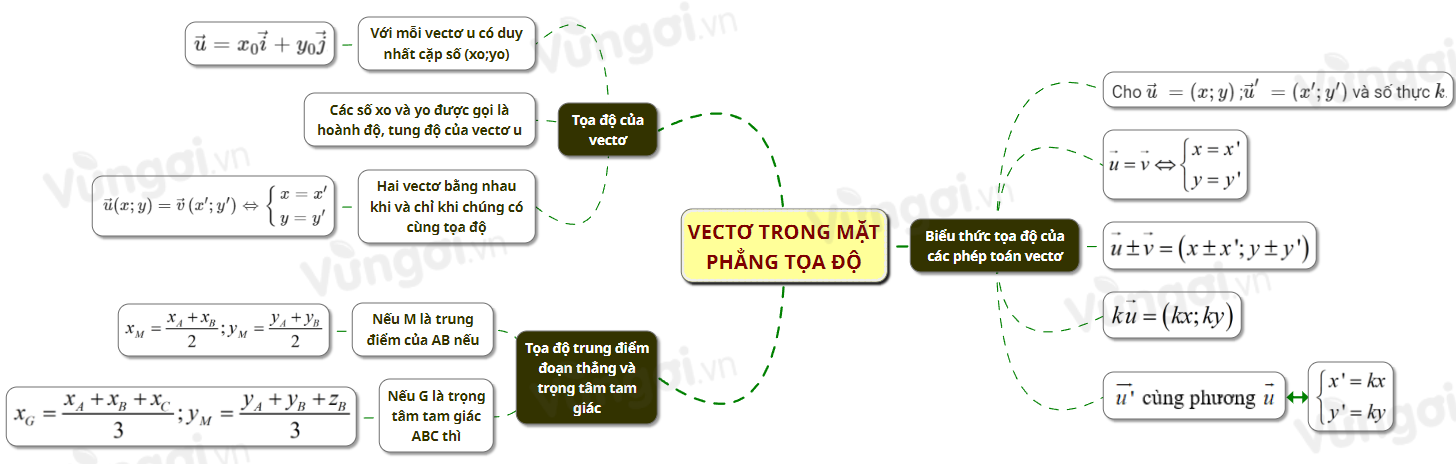
II. Tọa độ của vectơ
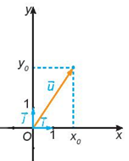
- Trên mặt phẳng, xét hai trục $Ox, Oy$ có chung gốc $O$ và vuông góc với nhau. Vectơ đơn vị của trục $Ox$ là \(\vec i\), vectơ đơn vị của trục $Oy$ là \(\vec j\).
- Hệ gồm hai trục $Ox, Oy$ như vậy được gọi là hệ trục tọa độ Oxy. Điểm \(O\) gọi là gốc toạ độ, trục Ox gọi là trục hoành, trục Oy gọi là trục tung. Mặt phẳng chứa hệ trục toạ độ Oxy gọi là mặt phẳng toạ độ \({\rm{Oxy}}\) hay mặt phẳng \({\rm{Oxy}}\).
- Với mỗi vectơ \(\vec u\) trên mặt phẳng Oxy, có duy nhất cặp số \(\left( {{x_0};{y_0}} \right)\) sao cho \(\vec u = {x_0}\vec i + {y_0}\vec j\).
- Ta nói vectơ \(\vec u\) có toạ độ \(\left( {{x_0};{y_0}} \right)\) và viết \(\vec u = \left( {{x_0};{y_0}} \right)\) hay \(\vec u\left( {{x_0};{y_0}} \right)\).
- Các số \({x_0},{y_0}\) tương ứng được gọi là hoành độ, tung độ của \(\vec u\).
Nhận xét:
Hai vectơ bằng nhau khi và chỉ khi chúng có cùng toạ độ.
\(\vec u(x;y) = \vec v\left( {{x^\prime };{y^\prime }} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {x^\prime }}\\{y = {y^\prime }}\end{array}} \right.\)
III. Biểu thức tọa độ của phép cộng hai vectơ, phép trừ hai vectơ, phép nhân một số với một vectơ
Cho \(\vec u{\rm{\;}} = (x;y)\) ;\(\vec u'{\rm{\;}} = (x';y')\) và số thực \(k\). Khi đó ta có:
1) \(\vec u = \vec u' \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = x'}\\{y = y'}\end{array}} \right.\)
2) \(\vec u{\rm{\;}} \pm \vec v{\rm{\;}} = (x \pm x';y \pm y')\)
3) \(k.\vec u{\rm{\;}} = (kx;ky)\)
4) \(\vec u'\) cùng phương \(\vec u\)(\(\vec u{\rm{\;}} \ne \vec 0\)) khi và chỉ khi có số \(k\) sao cho \(\left\{ {\begin{array}{*{20}{l}}{x' = kx}\\{y' = ky}\end{array}} \right.\)
Chú ý:
Điều kiện để hai véc tơ \(\overrightarrow u ,\overrightarrow v \) cùng phương là \(\dfrac{{{u_1}}}{{{v_1}}} = \dfrac{{{u_2}}}{{{v_2}}}\) với \({v_1}.{v_2} \ne 0\)
IV. Tọa độ trung điểm đoạn thẳng và tọa độ trọng tâm tam giác
a) Cho hai điểm \(A\left( {{x_A};{y_A}} \right)\) và \(B\left( {{x_B};{y_B}} \right)\). Nếu \(M\left( {{x_M};{y_M}} \right)\) là trung điểm đoạn thẳng $A B$ thì
\({x_M} = \dfrac{{{x_A} + {x_B}}}{2};{y_M} = \dfrac{{{y_A} + {y_B}}}{2}.\)
b) Cho tam giác $A B C$ có \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Nếu \(G\left( {{x_G};{y_G}} \right)\) là trọng tâm tam giác $ABC$ thì
\({x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}.\)

