I. Khái niệm hàm số bậc hai
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\).
Trong đó \(x\) là biến số, a, b, c là các hằng số.
TXĐ: \(D = \mathbb{R}\).
Ví dụ:
a) Hàm số \(y = 2{x^2} + x - 6\) và \(y = - 3{x^2} + 2\) là hàm số bậc hai.
b) Hàm số \(y = \dfrac{1}{{{x^2}}}\) không là hàm số bậc hai
II. Đồ thị hàm số bậc hai
- Có dáng là đường Parabol có đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right),\,\,\,\Delta = {b^2} - 4ac\).
- Trục đối xứng là đường thẳng \(x = - \dfrac{b}{{2a}}\).
- Bề lõm hướng lên trên khi \(a > 0\) và hướng xuống dưới khi \(a < 0\)
Chú ý: Điểm \(A\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = f\left( x \right) \Leftrightarrow {y_0} = f\left( {{x_0}} \right)\).
- Cách vẽ:
+) Xác định đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\).
+) Xác định trục đối xứng và hướng bề lõm của parabol.
+) Xác định một số điểm cụ thể của parabol (chẳng hạn giao điểm của parabol với các trục tọa độ và các điểm đối xứng với chúng qua trục đối xứng).
+) Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để “nối” các điểm đó lại.

III. Sự biến thiên của hàm số bậc hai
Cho hàm số bậc hai \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
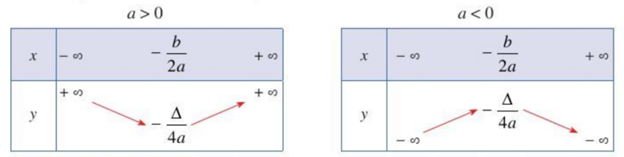
- Nếu \(a > 0\) thì hàm số đồng biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\), đạt được GTNN trên \(R\) tại \(x = - \dfrac{b}{{2a}}\).
- Nếu \(a < 0\) thì hàm số nghịch biến trên \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\), đồng biến trên \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\), đạt được GTLN trên \(R\) tại \(x = - \dfrac{b}{{2a}}\).
Ta có bảng biên thiên của hàm số bậc hai như sau:
Ví dụ:
a) Hàm số \(y = 2{x^2} + 5x - 1\) có: \(a = 2 > 0;\,\,b = 5;\,\,\, - \dfrac{b}{{2a}} = \dfrac{5}{4}\).
Vậy hàm số đã cho nghịch biến trên khoảng \(\left( { - \infty ;\dfrac{5}{4}} \right)\), đồng biến trên khoảng \(\left( {\dfrac{5}{4}; + \infty } \right)\).
b) Hàm số \(y = - 3{x^2} - 4x + 2\) có: \(a = - 3 < 0;\,\,b = - 4;\,\, - \dfrac{b}{{2a}} = - \dfrac{2}{3}\).
Vậy hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ; - \dfrac{2}{3}} \right)\), nghịch biến trên khoảng \(\left( { - \dfrac{2}{3}; + \infty } \right)\).
IV. Ứng dụng của hàm số bậc hai
1. Phương trình chuyển động của vật chuyển động thẳng biến đổi đều \(y = {x_0} + {v_0}t + \dfrac{{a{t^2}}}{2}\)
trong đó \({x_0}\) là toạ độ ban đầu của vật, \({v_0}\) là vận tốc ban đầu của vật và a là gia tốc của vật
Như vậy toạ độ x(t) của vật là một hàm số bậc hai của thời gian \(t\).
Khi đó độ cao (so với mặt đất) của vật tại thời điểm \(t\) cho bởi phương trình:
\(y(t) = {y_0} + {v_0}t - \dfrac{1}{2}g{t^2},\)
trong đó \({y_0}\) (mét) là độ cao ban đầu của vật khi ném lên, \({v_0}(\;{\rm{m}}/{\rm{s}})\) là vận tốc ban đầu của vật và \(g\) là gia tốc trọng trường \(\left( {g \approx 9,8\;{\rm{m}}/{{\rm{s}}^2}} \right)\).
Đặc biệt, khi bỏ qua sức cản không khí, nếu một vật rơi tự do từ độ cao \({y_0}\) (mét) so với mặt đất thì độ cao \(y\) (mét) của nó tại thời điểm \(t\) (giây) cho bởi công thức:
\(y(t) = {h_0} - \dfrac{1}{2}g{t^2}.\)
2. Phương trình chuyển động của vật ném xiên
Một vật được ném từ độ cao \(y_0\) (mét) so với mặt đất, với vận tốc ban đầu \({v_0}(\;{\rm{m}}/{\rm{s}})\) hợp với phương ngang một góc \(\alpha \). Khi đó quỹ đạo chuyển động của vật tuân theo phương trình
\(y = \dfrac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha + y_0\)
ở đó \(x\) (mét) là khoảng cách vật bay được theo phương ngang tính từ mặt đất tại điềm ném, \(y\) (mét) là độ cao so với mặt đất của vật trong quá trình bay, \(g\) là gia tốc trọng trường.
Như vậy quỹ đạo chuyển động của một vật ném xiên là một parabol.

