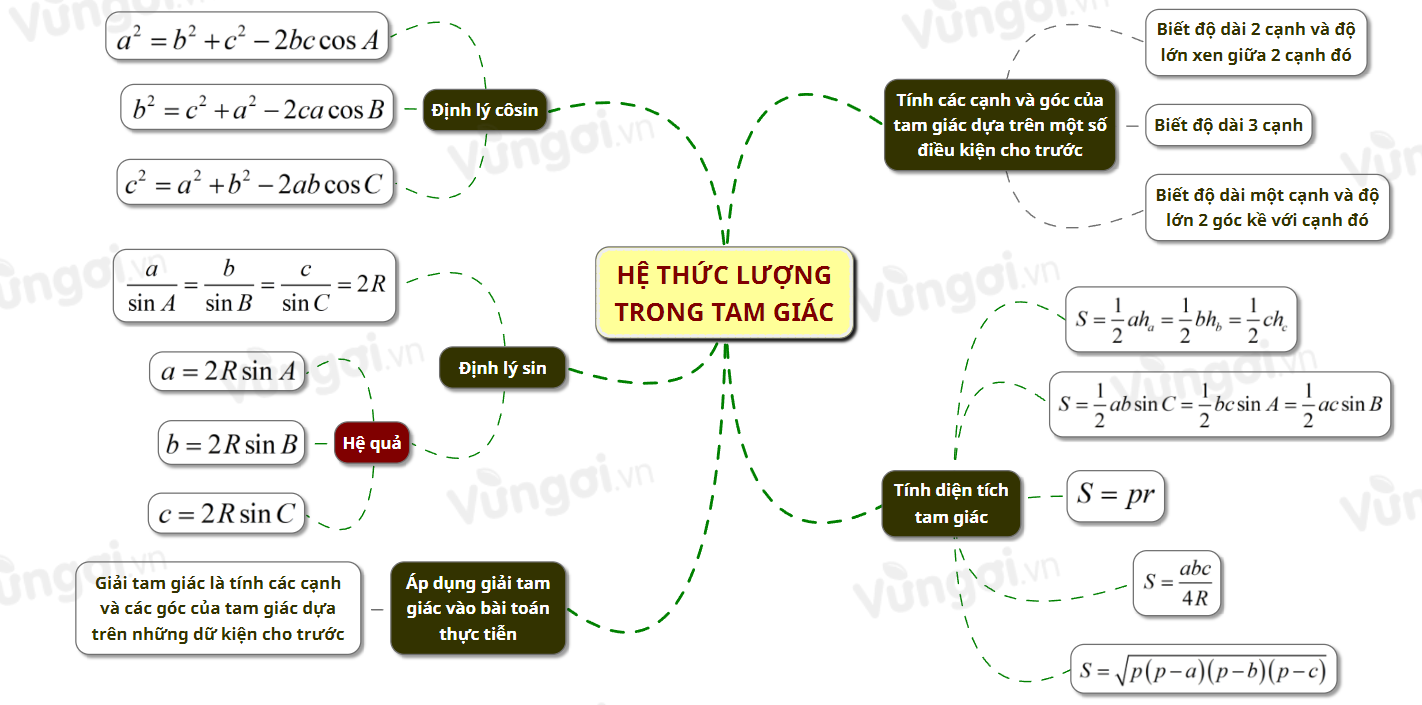
I. Sơ đồ tư duy Hệ thức lượng trong tam giác
II. Định lí côsin
Cho tam giác $A B C$ có \(BC = a,CA = b,AB = c\). Khi đó:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Hệ quả
\(\begin{array}{l}\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\\cos B = \dfrac{{{c^2} + {a^2} - {b^2}}}{{2ca}}\\\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\end{array}\)
III. Định lí sin
Cho tam giác \(ABC\;{\rm{ có }}\;BC = a,CA = b,AB = c\) và bán kính đường tròn ngoại tiếp là $R$. Khi đó:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
Hệ quả:
\(a = 2R\sin A\)
\(b = 2R\sin B\)
\(c = 2R\sin C\)
IV. Tính các cạnh và góc của tam giác dựa trên một số điều kiện cho trước
Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:
- Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;
- Biết độ dài ba cạnh;
- Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.
V. Tính diện tích tam giác
Cho tam giác $ABC$. Ta kí hiệu:
- \({h_a},{h_b},{h_c}\) là độ dài các đường cao lần lượt ứng với các cạnh $BC, CA, AB$.
- $R$ là bán kính đường tròn ngoại tiếp tam giác.
- $r$ là bán kính đường tròn nội tiếp tam giác.
- $p$ là nửa chu vi tam giác.
- S là diện tích tam giác.
Ta có các công thức tính diện tích tam giác sau:
1) \(S = \dfrac{1}{2}a{h_a} = \dfrac{1}{2}b{h_b} = \dfrac{1}{2}c{h_c}\);
2) \(S = \dfrac{1}{2}ab\sin C = \dfrac{1}{2}bc\sin A = \dfrac{1}{2}ac\sin B\);
3) \(S = \dfrac{{abc}}{{4R}}\);
4) \(S = pr\);
5) \(S = \sqrt {p(p - a)(p - b)(p - c)} \) (công thức Heron).
VI. Áp dụng giải tam giác vào bài toán thực tiễn
- Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.
- Vận dụng giải tam giác giúp ta giải quyết rất nhiều bài toán trong thực tế, đặc biệt là trong thiết kế và xây dựng.

