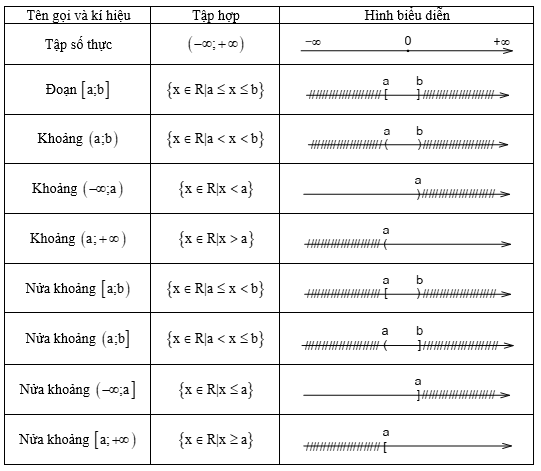
I. Sơ đồ tư duy Tập hợp và các phép toán trên tập hợp
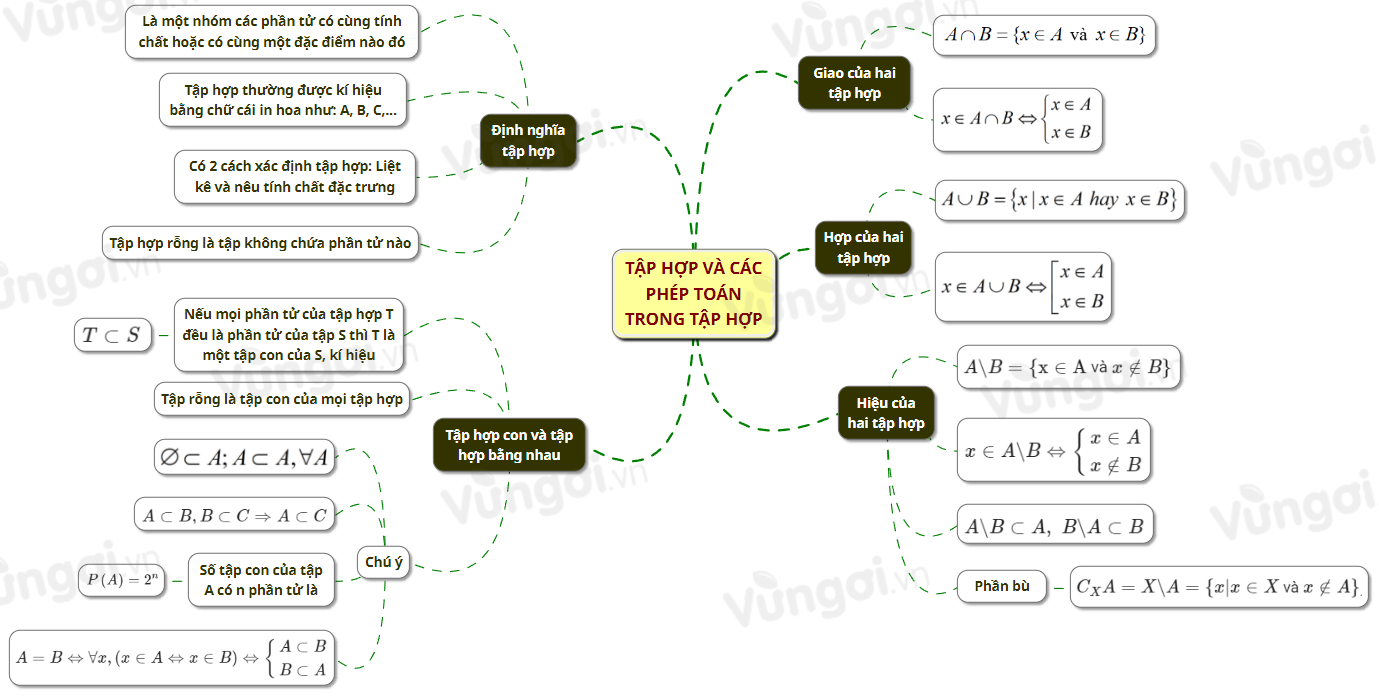
II. Định nghĩa tập hợp
1. Định nghĩa
Là một nhóm các phần tử có cùng tính chất hoặc có cùng một đặc điểm nào đó. Tập hợp thường được kí hiệu bằng chữ cái in hoa như: \(A,B,C,...\)
Chú ý: Cho tập hợp \(A\) .
+ Nếu \(a\) là phần tử thuộc tập \(A\) ta viết \(a \in A\)
+ Nếu \(a\) là phần tử không thuộc tập \(A\) ta viết \(a \notin A\)
2. Cách xác định tập hợp
Có 2 cách để xác định tập hợp:
a) Liệt kê: Viết tất cả các phần tử của tập hợp vào giữa dấu \(\left\{ {} \right\}\), các phần tử cách nhau bởi dấu “,”.
b) Nêu tính chất đặc trưng: Chỉ ra tính chất đặc trưng của các phần tử.
Ta thường minh họa tập hợp bằng một đường cong khép kín gọi là biểu đồ Ven.
Chú ý:
Số phần tử của tập hợp S được kí hiệu là \(n\left( S \right)\). Chẳng hạn, tập hợp \(A = \left\{ {0;2;4;6;8} \right\}\) Có 5 phần tử nên \(n\left( A \right) = 5\)
3. Tập hợp rỗng
Là tập hợp không chứa phần tử nào, kí hiệu là \(\emptyset \).
\(A \ne \emptyset \Leftrightarrow \exists x:x \in A\)
Ví dụ: Tập nghiệm của phương trình \({x^2} + 4 = 0\) là tập rỗng.
III. Tập hợp con và tập hợp bằng nhau
1. Tập con của một tập hợp
Nếu mọi phần tử của tập hợp \(T\) đều là phần tử của tập hợp \(S\) thì ta nói \(T\) là một tập hợp con (tập con) của \(S\) và viết là \(T \subset S\) (đọc là \(T\) chứa trong \(S\) hoặc \(T\) là tập con của \(S\) ).
Quy ước: Tập hợp rỗng \(\emptyset \) được coi là con của mọi tập hợp.
Nhận xét: \(A \subset B \Leftrightarrow \left( {\forall x \in A \Rightarrow x \in B} \right)\)
Chú ý:
+) \(\emptyset \subset A,\forall A\)
+) \({\rm{A}} \subset {\rm{A,}}\forall {\rm{A}}\)
+) \(A \subset B,B \subset C \Rightarrow A \subset C\) (bắc cầu).
+ Số tập con của một tập hợp: Tập hợp \(A\) gồm có \(n\) phần tử thì số tập con của tập hợp \(A\) là \(P\left( A \right) = {2^n}\).
2. Hai tập hợp bằng nhau
Hai tập hợp \(S\) và \(T\) được gọi là hai tập hợp bằng nhau nếu mối phần tử của \(T\) cũng là phần tử của tập hợp \(S\) và ngược lại. Kí hiệu là \(S = T\).
\(A = B \Leftrightarrow \forall x,\left( {x \in A \Leftrightarrow x \in B} \right) \Leftrightarrow \left\{ \begin{array}{l}A \subset B\\B \subset A\end{array} \right.\)
IV. Giao của hai tập hợp
Tập hợp gồm tất cả các phần tử vừa thuộc \(A\) vừa thuộc \(B\) được gọi là giao của \(A\) và \(B\), kí hiệu \(A \cap B\).
\(A \cap B = {\rm{\{ }}x \in A\) và \(x \in B{\rm{\} }}\) hay \(x \in A \cap B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \in B\end{array} \right.\)
Ví dụ: Cho tập hợp \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;2} \right\}\) thì \(A \cap B = \left\{ 1 \right\}\)
V. Hợp của hai tập hợp
Tập hợp gồm các phần tử thuộc \(A\) hoặc thuộc \(B\) được gọi là hợp của \(A\) và \(B\), kí hiệu \(A \cup B\).
\(A \cup B = \left\{ {x|x \in A\,{\rm{hay }}x \in B} \right\}\) hay \(x \in A \cap B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \in B\end{array} \right.\)
Ví dụ: Cho tập \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;2} \right\}\) thì \(A \cup B = \left\{ {1;2;3;4} \right\}\).
VI. Hiệu của hai tập hợp, phần bù của hai tập hợp
1. Hiệu của hai tập hợp
Hiệu của hai tập hợp A và B là tập hợp gồm các phần tử thuộc A nhưng không thuộc B, kí hiệu là A\B.
\(A\backslash B = {\rm{\{ x}} \in {\rm{A}}\) và \(x \notin B{\rm{\} }}\) hay \(x \in A\backslash B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \notin B\end{array} \right.\)
Ví dụ: Cho tập \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;2} \right\}\) thì \(A\backslash B = \left\{ {3;4} \right\}\) và \(B\backslash A = \left\{ 2 \right\}\)
Chú ý: \(A\backslash B \subset A,\,\,B\backslash A \subset B\)
2. Phần bù
Cho tập hợp A là tập con của tập hợp X. Tập hợp những phần tử của X mà không phải là phần tử của A được gọi là phần bù của A trong X, kí hiệu là \({C_X}A\).
Vậy \({C_X}A = X\backslash A = {\rm{\{ }}x|x \in X\) và \(x \notin A{\rm{\} }}\).
Ví dụ: Cho tập \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;3} \right\}\) thì \({C_A}B = A\backslash B = \left\{ 4 \right\}\).
Minh họa các phép toán trên tập hợp bằng biểu đồ Ven:
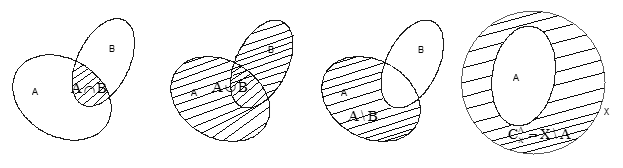
VII. Các tập hợp số
1. Nhắc lại các hàm số đã học
+ Tập các số tự nhiên: \(\mathbb{N} = \left\{ {0,1,2,...} \right\}\)
+ Tập các số tự nhiên khác 0: \({\mathbb{N}^*} = \left\{ {1,2,3,...} \right\}\)
+ Tập các số nguyên: \(\mathbb{Z} = \left\{ {..., - 2, - 1,0,1,2,...} \right\} = \left\{ {0, \pm 1, \pm 2,...} \right\}\)
+ Tập các số hữu tỉ: \(Q = \left\{ {\dfrac{m}{n}|m \in \mathbb{Z},n \in {\mathbb{Z}^*}} \right\}\)
+ Tập số vô tỉ \(I\)
+ Tập các số thực: \(\mathbb{R} = \left( { - \infty ; + \infty } \right)\) gồm tất cả các số trên kể cả số vô tỉ.
Mối quan hệ giữa các tập hợp số:
\({\mathbb{N}^*} \subset \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
2. Các tập con của \(\mathbb{R}\)