I. Sơ đồ tư duy Tích vô hương của hai vectơ_kntt
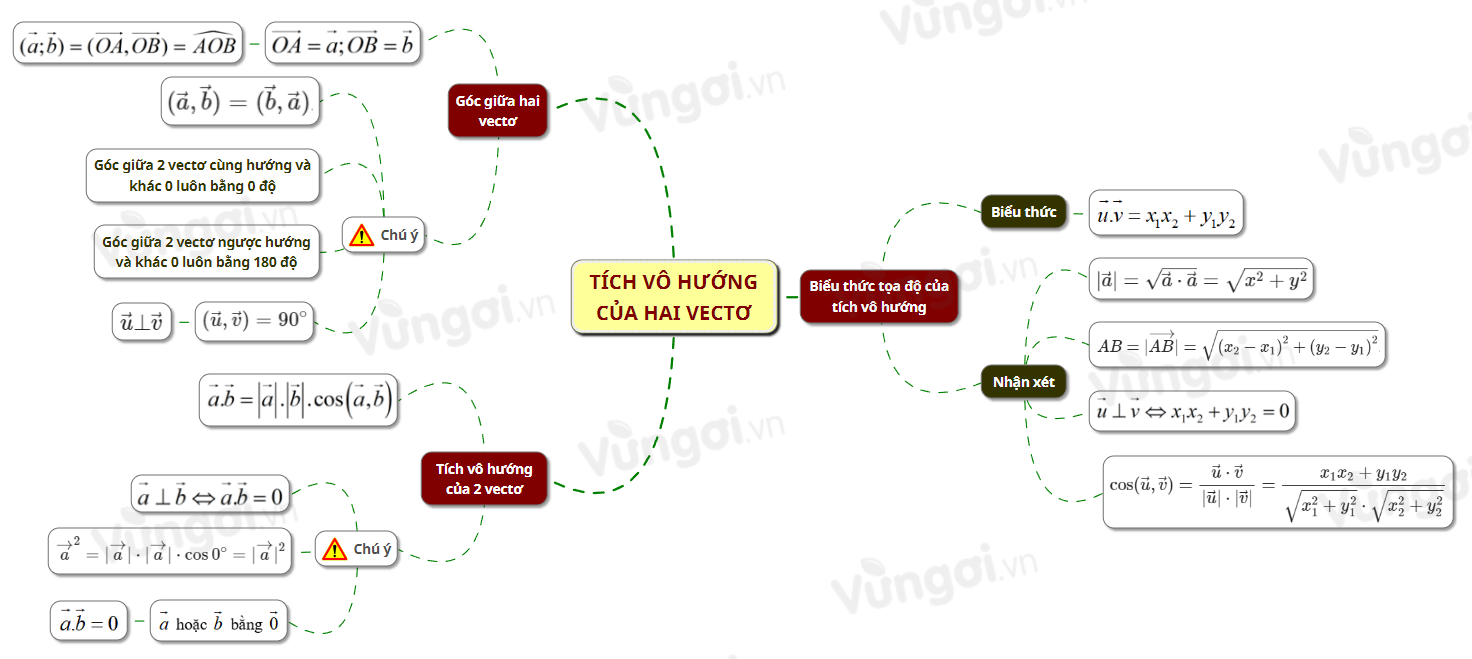
II. Tích vô hướng của hai vectơ
Tích vô hướng của hai véc tơ \(\overrightarrow a \) và \(\overrightarrow b \) là một số, kí hiệu là \(\overrightarrow a .\overrightarrow b \), được xác định bởi công thức: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Chú ý:
- \(\vec a \bot \vec b \Leftrightarrow \vec a \cdot \vec b = 0\).
- \(\overrightarrow a .\overrightarrow a \) còn được viết là \({\overrightarrow a ^2}\) và được gọi là bình phương vô hướng của vectơ \(\overrightarrow a \). Ta có \({\overrightarrow a ^2} = |\overrightarrow a | \cdot |\overrightarrow a | \cdot \cos {0^\circ } = |\overrightarrow a {|^2}\).
- Trường hợp ít nhất một trong hai vecto \(\vec a\) và \(\vec b\) bằng \(\vec 0\), ta quy ước \(\vec a \cdot \vec b = 0\).
III. Góc giữa hai vectơ
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) đều khác \(\overrightarrow 0 \). Từ một điểm \(O\) bất kì ta vẽ \(\overrightarrow {OA} = \overrightarrow a ;\,\,\overrightarrow {OB} = \overrightarrow b \)
Khi đó, số đo của góc AOB được gọi là số đo góc giữa hai véc tơ \(\overrightarrow a ,\overrightarrow b \)
Kí hiệu: \(\left( {\overrightarrow a ;\overrightarrow b } \right) = \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = \widehat {AOB}\).
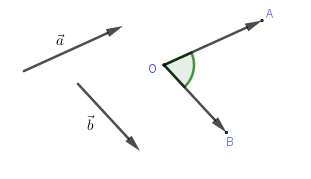
+ Quy ước : Nếu \(\overrightarrow a = \overrightarrow 0 \) hoặc \(\overrightarrow b = \overrightarrow 0 \) thì ta xem góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là tùy ý (từ \({0^0}\) đến \({180^0}\)).
Chú ý:
- Từ định nghĩa ta có \((\vec a,\vec b) = (\vec b,\vec a)\).
- Góc giữa hai vectơ cùng hướng và khác 0 luôn bằng \({0^\circ }\).
- Góc giữa hai vectơ ngược hướng và khác \(\vec 0\) luôn bằng \({180^\circ }\).
- Nếu \((\vec u,\vec v) = {90^\circ }\) thì ta nói rằng \(\vec u\) và \(\vec v\) vuông góc với nhau, kí hiệu là \(\vec u \bot \vec v\) hoặc \(\vec v \bot \vec u\). Đặc biệt \(\vec 0\) được coi là vuông góc với mọi vectơ.
IV. Biểu thức tọa độ của tích vô hướng
Nếu \(\vec u = \left( {{x_1};{y_1}} \right)\) và \(\vec v = \left( {{x_2};{y_2}} \right)\) thì \(\vec u \cdot \vec v = {x_1}{x_2} + {y_1}{y_2}\).
Nhận xét
a) Nếu \(\vec a = (x;y)\) thì \(|\vec a| = \sqrt {\vec a \cdot \vec a} = \sqrt {{x^2} + {y^2}} \).
b) Nếu \(A\left( {{x_1};{y_1}} \right)\) và \(B\left( {{x_2};{y_2}} \right)\) thì \(AB = |\overrightarrow {AB} | = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \).
c) Với hai vectơ \(\vec u = \left( {{x_1};{y_1}} \right)\) và \(\vec v = \left( {{x_2};{y_2}} \right)\) khác \(\vec 0\), ta có:
+) \(\vec u\) và \(\vec v\) vuông góc với nhau khi và chỉ khi \({x_1}{x_2} + {y_1}{y_2} = 0\).
+) \(\cos (\vec u,\vec v) = \dfrac{{\vec u \cdot \vec v}}{{|\vec u| \cdot |\vec v|}} = \dfrac{{{x_1}{x_2} + {y_1}{y_2}}}{{\sqrt {x_1^2 + y_1^2} \cdot \sqrt {x_2^2 + y_2^2} }}.\)

