I. Sơ đồ tư duy Các khái niệm mở đầu
II. Khái niệm vectơ
- Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Vectơ có điểm đầu là A, điểm cuối là B ta kí hiệu : \(\overrightarrow {AB} \)
Vectơ còn được kí hiệu là: \(\overrightarrow a ,{\rm{ }}\overrightarrow b ,{\rm{ }}\overrightarrow x ,{\rm{ }}\overrightarrow y ,...\)
- Độ dài đoạn thẳng \(AB\) gọi là độ dài véc tơ \(\overrightarrow {AB} \), kí hiệu \(\left| {\overrightarrow {AB} } \right|\). Vậy \(\left| {\overrightarrow {AB} } \right| = AB\).
III. Vectơ cùng phương, vectơ cùng hướng
Đường thẳng đi qua điểm đầu và điểm cuối của vectơ gọi là giá của vectơ
Hai vectơ có giá song song hoặc trùng nhau gọi là hai vectơ cùng phương
Nhận xét:
Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng.
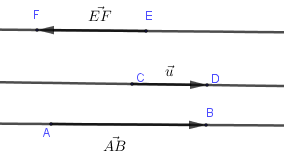
Ví dụ: Ở hình vẽ trên trên (hình 2) thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng còn \(\overrightarrow {EF} \) và \(\overrightarrow {CD} \) ngược hướng.
IV. Hai vectơ bằng nhau
Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài
Nhận xét: Khi cho trước vectơ \(\vec a\) và điểm \(O\), thì ta luôn tìm được một điểm \(A\) duy nhất sao cho \(\overrightarrow {OA} = \vec a\).
Vectơ đối của vectơ \(\overrightarrow a \) là vectơ ngược hướng và có cùng độ dài với vectơ \(\overrightarrow a \)
Kí hiệu: \( - \overrightarrow a \)
Như vậy \(\overrightarrow a + \left( { - \overrightarrow a } \right) = \overrightarrow 0 {\rm{, }}\forall \overrightarrow a \) và \(\overrightarrow {AB} = - \overrightarrow {BA} \)
Ví dụ: Cho hình bình hành \(ABDC\) khi đó \(\overrightarrow {AB} = \overrightarrow {CD} \), \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \) là hai vectơ đối nhau.
V. Vectơ - không
Vectơ – không là vectơ có điểm đầu trùng điểm cuối. Kí hiệu là \(\overrightarrow 0 \)
Chú ý:
- Quy ước vectơ-không có độ dài bằng 0.
- Vectơ-không luôn cùng phương, cùng hướng với mọi vectơ.
- Mọi vectơ-không đều bằng nhau: \(\vec 0 = \overrightarrow {AA} = \overrightarrow {BB} = \overrightarrow {CC} = \ldots \) với mọi điểm \(A,B,C, \ldots \)
- Vectơ đối của vectơ-không là chính nó.
VI. Biểu thị một số đại lượng có hướng bằng vectơ
- Ta có thể dùng vectơ để biểu diễn các đại lượng: như lực, vận tốc, gia tốc…
- Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.

