Phương pháp quy nạp toán học

I. Phương pháp quy nạp toán học

Chứng minh một mệnh đề toán học phụ thuộc \(n \in \mathbb{N}*,\) đúng với mọi \(n \in \mathbb{N}*,\) bằng phương pháp quy nạp toán học, gồm hai bước sau:

Chú ý: Nếu phải chứng minh một mệnh đề đúng với mọi số tự nhiên \(n \ge p\) (\(p\) là một số tự nhiên nào đó) thì:

Ví dụ: Chứng minh rằng \({n^3} - n\) chia hết cho 3 với mọi \(n \in {\mathbb{N}^*}\).

Giải

Bước 1. Khi \(n = 1\), ta có: \({1^3} - 1 = 0\) chia hết cho 3 .

Bước 2. Với \(k\) là một số nguyên dương tuỳ ý mà \({k^3} - k\) chia hết cho 3 , ta phải chứng minh \({(k + 1)^3} - (k + 1)\) chia hết cho 3 .

Thật vậy, ta có: \({(k + 1)^3} - (k + 1) = {k^3} + 3{k^2} + 3k + 1 - k - 1 = {k^3} - k + 3\left( {{k^2} + k} \right)\).

Theo giả thiết quy nạp: \({k^3} - k:3\), mà \(3\left( {{k^2} + k} \right) \vdots 3\).

Suy ra \({k^3} - k + 3\left( {{k^2} + k} \right) \vdots 3\), tức là \({(k + 1)^3} - (k + 1) \vdots 3\).

Do đó, theo nguyên lí quy nạp toán học, \({n^3} - n\) chia hết cho 3 với mọi \(n \in {\mathbb{N}^*}\).

II. Ứng dụng phương pháp quy nạp toán học

Phương pháp quy nạp toán học được sử dụng trong nhiều lĩnh vực toán học khác nhau (số học, đại số, hình học, giải tích, ...). Dưới đây, ta xét thêm một vài ứng dụng.

Ví dụ 1:

Sử dụng phương pháp quy nạp toán học, chứng minh rằng tổng các góc trong của một đa giác \(n\) cạnh \((n \ge 3)\) là \((n - 2) \cdot {180^\circ }\).

Giải. Ta chứng minh khẳng định trên bằng quy nạp theo \(n\), với \(n \ge 3\).

- Với \(n = 3\), ta có tổng ba góc của một tam giác bằng \({180^\circ } = (3 - 2){.180^\circ }\).

Vậy khẳng định đúng với \(n = 3\).

- Giả sử khẳng định đúng với \(n = k \ge 3\), ta sẽ chứng minh nó đúng với \(n = k + 1\).

Thật vậy, xét đa giác \(k + 1\) cạnh \({A_1}{A_2} \ldots {A_k}{A_{k + 1}}\), nối hai đỉnh \({A_1}\) và \({A_k}\) ta được đa giác \(k\) cạnh \({A_1}{A_2} \ldots {A_k}\).

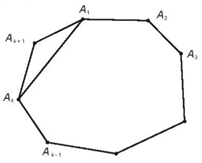
Theo giả thiết quy nạp, tổng các góc của đa giác \(k\) cạnh này bằng \((k - 2){.180^\circ }.\)

Dễ thấy tổng các góc của đa giác \({A_1}{A_2} \ldots {A_k}{A_{k + 1}}\) bằng tổng các góc của đa giác \({A_1}{A_2} \ldots {A_k}\) cộng với tổng các góc của tam giác \({A_{k + 1}}{A_k}{A_1}\), tức là bằng

\((k - 2){.180^\circ } + {180^\circ } = (k - 1){.180^\circ } = [(k + 1) - 2]{.180^\circ }.\)

Vậy khẳng định đúng với mọi đa giác \(n\) cạnh, \(n \ge 3\).

Ví dụ 2:

Một người gửi số tiền \(A\) (đồng) vào ngân hàng với lãi suất \(r\% /\) năm. Biết rằng, nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm, số tiền lãi sẽ được nhập vào vốn ban đầu. Chứng minh số tiền nhận được (bao gồm cả vốn lẫn lãi) sau \(n\) (năm) là \({T_n} = A{\left( {1 + \dfrac{r}{{100}}} \right)^n}\) (đồng), nếu trong khoảng thời gian này người gửi không rút tiền ra và lãi suất không thay đổi.

Giải

Sau 1 năm, số tiền vốn và lãi thu được là: \(A + A \cdot \dfrac{r}{{100}} = A\left( {1 + \dfrac{r}{{100}}} \right)\) (đồng).

Vậy \({T_1} = A{\left( {1 + \dfrac{r}{{100}}} \right)^1}\), tức là đẳng thức đúng với \(n = 1\).

Với \(k\) là một số nguyên dương tùy ý mà đẳng thức đúng, ta phải chứng minh đẳng thức cũng đúng với \(k + 1\), tức là \({T_{k + 1}} = A{\left( {1 + \dfrac{r}{{100}}} \right)^{k + 1}}\).

Thật vậy, theo giả thiết quy nạp, ta có: \({T_k} = A{\left( {1 + \dfrac{r}{{100}}} \right)^k}\).

Ta thấy, sau khi hết \(k\) (năm) thì số tiền \({T_k} = A{\left( {1 + \dfrac{r}{{100}}} \right)^k}\) trở thành tiền vốn để tính tiền lãi cho năm thứ \(k + 1\). Do đó, số tiền vốn và lãi người đó có được sau \(k + 1\) (năm) là:

\(A{\left( {1 + \dfrac{r}{{100}}} \right)^k} + A{\left( {1 + \dfrac{r}{{100}}} \right)^k} \cdot \dfrac{r}{{100}} = A{\left( {1 + \dfrac{r}{{100}}} \right)^k}\left( {1 + \dfrac{r}{{100}}} \right) = A{\left( {1 + \dfrac{r}{{100}}} \right)^{k + 1}}{\rm{, }}\)

tức là \({T_{k + 1}} = A{\left( {1 + \dfrac{r}{{100}}} \right)^{k + 1}}\) (đồng).

Vậy đẳng thức đúng với \(k + 1\).

Do đó, theo nguyên lí quy nạp toán học, đẳng thức đúng với mọi \(n \in {\mathbb{N}^*}\), tức là số tiền cả vốn lẫn lãi người đó có được sau \(n\) (năm) là:

\({T_n} = A{\left( {1 + \dfrac{r}{{100}}} \right)^n}{\rm{. }}\)