I. Mạch R, L, C mắc nối tiếp
Điện áp và tổng trở của mạch:
\(\left\{ \begin{array}{l}U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} \to {U_0} = \sqrt {U_{0R}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} \\Z = \sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \end{array} \right.\)
Định luật Ohm cho mạch:
\(\left\{ \begin{array}{l}I = \frac{U}{Z} = \frac{{\sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} }}{{\sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{{U_R}}}{R} = \frac{{{U_L}}}{{{Z_L}}} = \frac{{{U_C}}}{{{Z_C}}} = \frac{{{I_0}}}{{\sqrt 2 }}\\{I_0} = \frac{{{U_0}}}{Z} = \frac{{\sqrt {U_{0R}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} }}{{\sqrt {R_{}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{{U_{0R}}}}{R} = \frac{{{U_{0L}}}}{{{Z_L}}} = \frac{{{U_{0C}}}}{{{Z_C}}} = I\sqrt 2 \end{array} \right.\)
Độ lệch pha của điện áp và cường độ dòng điện trong mạch là φ, được cho bởi:
\(\tan \varphi = \frac{{{U_L} - {U_C}}}{{{U_R}}} = \frac{{{Z_L} - {Z_C}}}{R}\);\(\varphi =\varphi_u - \varphi_i\)
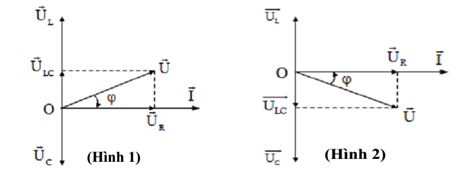
- Khi UL > UC hay ZL > ZC thì u nhanh pha hơn i góc φ. (Hình 1). Khi đó ta nói mạch có tính cảm kháng.
- Khi UL < UC hay ZL < ZC thì u chậm pha hơn i góc φ. (Hình 2). Khi đó ta nói mạch có tính dung kháng.
Giản đồ véc tơ (Giản đồ Frenen):
II. Pha u, i – Viết phương trình u, i
*Phương pháp đại số
Bước 1: Xác định các giá trị I0, U0, ω
\({U_0} = {I_0}Z = \sqrt {{U_{0R}}^2 + {{\left( {{U_{0L}} - {U_{0C}}} \right)}^2}} \)
\(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Bước 2: Xác định pha φu, φi
\(\tan \varphi = \tan \left( {{\varphi _u} - {\varphi _i}} \right) = \frac{{{Z_L} - {Z_C}}}{R}\)
+ \(\varphi > 0 \to {\varphi _u} > {\varphi _i}\) : u sớm pha φ so với i (ZL>ZC: mạch có tính cảm kháng)
+ \(\varphi < 0 \to {\varphi _u} < {\varphi _i}\): u chậm pha φ so với i (ZL<ZC: mạch có tính dung kháng)
+ \(\varphi = 0 \to {\varphi _u} = {\varphi _i}\): u cùng pha với i (ZL=ZC: cộng hưởng điện)
Bước 3: Viết phương trình u, i theo đầu bài
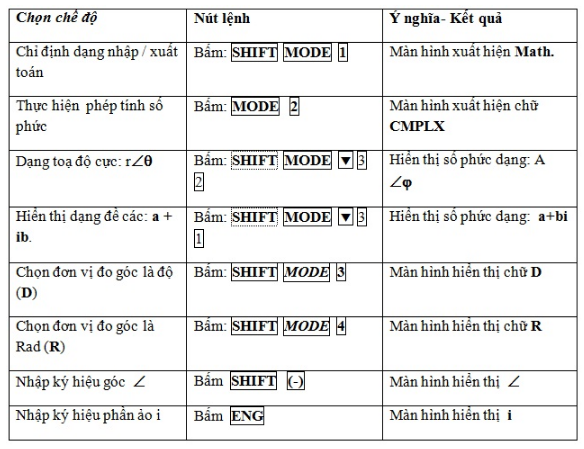
*Phương pháp vận dụng số phức ( Sử dụng máy tính casio fx570ES)
Cường độ dòng điện:
\(i = {I_0}{\rm{cos}}\left( {\omega t + {\varphi _i}} \right) \Rightarrow i = {I_0}\angle {\varphi _i}\)
Điện áp:
\(u = {U_0}{\rm{cos}}\left( {\omega t + {\varphi _i}} \right) \Rightarrow u = {U_0}\angle {\varphi _u}\)
Liên hệ giữa u và i:
u=i\(\overline Z \)=i(R+(ZL-ZC) i) - trong đó: i là phần ảo của số phức
