Đề thi học kì 2 Toán lớp 9 trường THPT chuyên Hà Nội Amsterdam - Đề sưu tầm số 10

ĐỀ THI HỌC KÌ II – THPT CHUYÊN HÀ NỘI AMSTERDAM

Môn: Toán 9

Năm học: 2019 - 2020

Thời gian: 90 phút

Bài 1: Cho hai biểu thức: $A=\frac{x-7}{\sqrt{x}}$ và $B=\frac{1}{\sqrt{x}+2}+\frac{\sqrt{x}}{2-\sqrt{x}}+\frac{2x-\sqrt{x}+2}{x-4}$ với $x>0,x\ne 4$

1) Tính giá trị của A khi x=9.

2) Rút gọn biểu thức B

3) Tìm tất cả các giá trị nguyên của x để biểu thức P = A.B nguyên.

Bài 2:

1) Giải bài toán bằng cách lập phương trình và hệ phương trình:

Một ca nô đi xuôi dòng 54km và ngược dòng 46km và tổng thời gian cả đi lẫn về là 4 giờ. Nếu ca nô đi xuôi dòng 81km và ngược dòng 23km thì tổng thời gian cả đi lẫn về là 4 giờ. Tính vận tốc riêng của ca nô và vận tốc dòng nước biết các vận tốc này là không đổi.

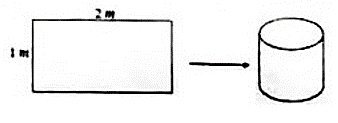
2) Mặt xung quanh của một thùng chứa nước hình trụ có chiều cao 1m được gò từ một tấm tôn hình chữ nhật có kích thước 1mx2m (như hình vẽ). Hỏi thùng nước này đựng đầy được bao nhiêu mét khối nước? ( Bỏ qua bề dày của tấm tôn, lấy $\pi =3,14$ và làm tròn đến chữ số thập phân thứ hai).

Bài 3:

1) Giải phương trình $x+7\sqrt{x}-8=0$.

2) Trong mặt phẳng tọa độ Oxy, cho Parabol (P): $y=x^2$và đường thẳng (d): y = mx+4 (m là tham số).

a) Chứng minh đường thẳng (d) cắt đồ thị (P) tại hai điểm phân biệt.

b) Gọi $x_1,x_2$ là hoành độ của hai giao điểm trên. Tìm giá trị của m để $\sqrt{-x_1}=\sqrt{4x_2}$

Bài 4: Cho nửa đường tròn (O) đường kính BC và dây cung EF sao cho các điểm F, C nằm khác phía so với đường thẳng BE. Hai dây cung BE và CF cắt nhau tại H, tia BF và CE cắt nhau tại A. Đường thẳng AH cắt đường thẳng BC tại D.

1) Chứng minh AEDB là tứ giác nội tiếp.

2) Gọi S là giao điểm của EF và CB. Chứng minh FB là tia phân giác của góc SFD.

3) Chứng minh $\frac{SB}{SC}=\frac{DB}{DC}$.

4) Giả sử AB < AC. Tiếp tuyến tại B của nửa đường tròn (O) cắt CF tại P, tiếp tuyến tại của nửa đường tròn (O) cắt BE tại Q. Chứng minh 3 điểm S, P, Q thẳng hàng.

Bài 5:

Với các số thực không âm $a,b,c$ thỏa mãn $a + b + c = 3$. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=ab+bc+ca-\frac{1}{2}abc$.