Đề thi học kì 2 Toán lớp 9 - Đề sưu tầm số 5

ĐỀ THI HỌC KỲ II

Môn Toán Lớp 9

Thời gian: 90 phút

Đề: 05

A. TRẮC NGHIỆM : (3 điểm)

I. Chọn câu trả lời em cho là đúng nhất:

Câu 1: Trong các cặp số sau đây, cặp số nào là nghiệm của phương trình 3x + 5y = –3? 

A. (–2; 1)              B. (0; –1)              C. (–1; 0)              D. (1; 0)

Câu 2. Cho đường tròn (O; 2cm), độ dài cung 60⁰ của đường tròn này là:

       A. $\frac{\pi }{3}$cm                  B.$\frac{3\pi }{2}$cm                C.$\frac{\pi }{2}$cm                 D.$\frac{2\pi }{3}$cm

Câu 3: Nghiệm của hệ phương trình $\left\{\begin{array}{l}2x-3y=3\\ x+3y=6\end{array}\right.$là:

A.(2;1)                  B.( 3;1)                 C(1;3)                            D.(3; -1)

Câu 4: Đường kính vuông góc với một dây cung thì:

A. Đi qua trung điểm của dây cung ấy.                B. không đi qua trung điểm của dây cung ấy

Câu 5: Phương trình x² - 7x – 8 = 0. có tổng hai nghiệm là:

A.8                       B.-7                      C.7                       D.3,5                 

Câu 6: Cho hình vẽ: 

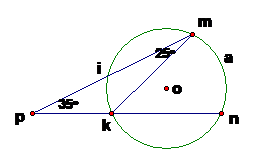
Số đo của cung bằng:                                                                                           

A. 60⁰                   B. 70⁰                 

C. 120⁰                 D.130⁰     

Câu 7: Phương trình của parabol có đỉnh tại gốc tọa độ và đi qua điểm ( - 1 ; 3 ) là:

     A.  y = x²                            B. y = - x²             C. y = -3x²             D. y = 3x²

Câu 8: Tứ giác ABCD nội tiếp đường tròn có  = 50⁰;   = 70⁰ . Khi đó   -  bằng:

     A. 30⁰              B . 20⁰                            C . 120⁰                D . 140⁰

II.  Điền đúng (Đ) hoặc sai (S) vào ô vuông ở cuối mỗi câu sau: (1 điểm)

B. TỰ LUẬN (7 điểm)                                                                                

Bài 1. (2 điểm) Giải hệ phương trình sau:

Bài 2. (1 điểm)

Tìm các giá trị của m để phương trình 2x² – (4m + 3)x + 2m² –1 = 0 có nghiệm.

Bài 3. (1 điểm)

Một xe khách và một xe du lịch khởi hành cùng một lúc từ A đến B. Xe du lịch có vận tốc lớn hơn vận tốc của xe khách là 20 km/h, do đó nó đến B trước xe khách 25 phút. Tính vận tốc của mỗi xe, biết khoảng cách AB là 100 km.

Bài 4. (3 điểm)

Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi E, D lần lượt là giao điểm của các tia phân giác trong và ngoài của hai góc B và C. Đường thẳng ED cắt BC tại I, cắt cung nhỏ BC ở M. Chứng minh:

a. Ba điểm A, E, D thẳng hàng.

b.Tứ giác BECD nội tiếp được trong đường tròn.

c. BI. IC = ID. IE

ĐÁP ÁN

A. TRẮC NGHIỆM ( 3 điểm):

I.

II. Điền Đ hoặc S vào chỗ trống:

          1- Sai                    2 - Đúng                         3 - Đúng                         4 - Sai        

B. TỰ LUẬN: (7 điểm).

Bài 1:

a) Giải hệ phương trình 

  $\begin{array}{l}\left\{\begin{array}{l}2x-3y=1\\ x-4y=-7\end{array}\right.\\ \iff \left\{\begin{array}{l}2x-3y=1\\ 2x-8y=-14\end{array}\right.\\ \iff \left\{\begin{array}{l}2x-3y=1\\ 5y=-15\end{array}\right.\\ \iff \left\{\begin{array}{l}2x-3y=1\\ y=-3\end{array}\right.\\ \iff \left\{\begin{array}{l}2x-3.\left(-3\right)=1\\ y=-3\end{array}\right.\\ \iff \left\{\begin{array}{l}x=-4\\ y=-3\end{array}\right.\end{array}$      

Vậy hệ phương trình có một nghiệm là $\left(x;y\right)=\left(-4;-3\right)$

Bài 2:  Xét phương trình: 2x² – (4m + 3)x + 2m² –1 = 0

Ta có: $\Delta ={\left[-\left(4m+3\right)\right]}^2-4.2.\left(2m^2-1\right)=24m+17$

Để phương trình đã cho có nghiệm khi $\Delta \ge 0\iff 24m+17\ge 0\iff m\ge -\frac{17}{24}$.

Bài 3:

Gọi vận tốc của xe khách là x (km/h), (ĐK: x > 0)

khi đó vận tốc của xe du lịch là x+20 (km/h)

Thời gian đi từ A đến B của xe khách là : $\frac{100}{x}$  (giờ)

Thời gian đi từ A đến B của xe du lịch là : $\frac{100}{x+20}$  (giờ)

Vì xe du lịch đến B  trước xe khách 25 phút = $\frac{5}{12}$giờ nên ta có phương trình:

$\begin{array}{l}\frac{100}{x}-\frac{100}{x+20}=\frac{5}{12}\iff \frac{100\left(x+20\right)}{x\left(x+20\right)}-\frac{100x}{x\left(x+20\right)}=\frac{5}{12}\\ \iff \frac{100\left(x+20\right)-100x}{x\left(x+20\right)}=\frac{5}{12}\\ \iff \frac{2000}{x\left(x+20\right)}=\frac{5}{12}\\ \iff 12.2000=5x\left(x+20\right)\\ \iff 5x^2+100x-24000=0\\ \iff \left[\begin{array}{l}x=60(\mathrm{t}/\mathrm{m})\\ x=-80(\mathrm{loa}¨\mathrm{ii})\end{array}\right.\end{array}$

Vậy vận tốc của xe du lịch là: 80km/h và vận tốc của xe khách là 60km/h.

Bài 4:

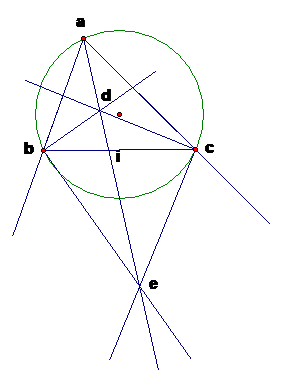
a) Vì E là giao điểm hai phân giác góc B và C của tam giác ABC nên AE cũng là phân giác của góc A. Khi đó  AE và AD đều là phân giác trong của góc BAC nên A, E, D thẳng hàng     

b) Gọi Bx là tia đối của tia BA

Ta có: $\widehat{ABD}=\widehat{CBD}=\frac{1}{2}\widehat{ABC}$  (BD là phân giác góc  ABC)

và $\widehat{CBE}=\widehat{xBE}=\frac{1}{2}\widehat{xBC}$  (BD là phân giác góc xBC)

$\Rightarrow \widehat{DBE}=\widehat{DBC}+\widehat{CBE}=\frac{1}{2}\left(\widehat{ABC}+\widehat{xBC}\right)=\frac{1}{2}.180°=90°$

Chứng minh tương tự ta được

Ta có: $\widehat{EBD}$  + $\widehat{ECD}$  = 90⁰ + 90⁰ = 180⁰ 

   Tứ giác BECD nội tiếp đường tròn 

c) Xét hai tam giác BIE và tam giác DIC:

  $\widehat{EBC}$  = $\widehat{EDC}$  (haigóc nội tiếp cùng chắn cung EC)

$\widehat{BIE}$ = $\widehat{DIC}$  ( đối đỉnh)

  $∆$BIE ~ $∆$DIC ( g-g) $\Rightarrow$ $\frac{BI}{ID}=\frac{IE}{IC}$ $\Rightarrow$ BI. IC = IE. ID .