Trường hợp bằng nhau thứ hai và thứ ba của tam giác

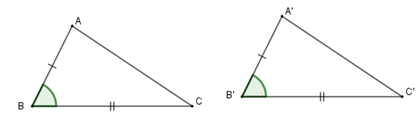
I. Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh

Ví dụ:

$\left. \begin{array}{l}AB = A'B'\\\widehat B = \widehat B'\\BC = B'C'\end{array} \right\}$$\Rightarrow \Delta ABC = \Delta A'B'C'\left( {c.g.c} \right)$

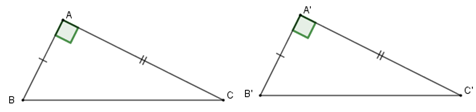
Hệ quả:

Nếu hai cạnh góc vuông của tam giác vuông này bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Ví dụ:

Cho tam giác $ABC$ vuông tại $A$, tam giác $A'B'C'$ vuông tại $A'.$ Khi đó

$\left. \begin{array}{l}AB = A'B'\\AC = A'C'\end{array} \right\}$$\Rightarrow \Delta ABC = \Delta A'B'C'.$

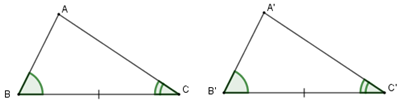
II. Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc

Ví dụ:

 $\left. \begin{array}{l}\widehat B = \widehat B'\\BC = B'C'\\\widehat C = \widehat C'\end{array} \right\}$$\Rightarrow \Delta ABC = \Delta A'B'C'\,\,(g.c.g)$