I. Hai góc kề bù
Hai góc có một cạnh chung, 2 cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.
Tính chất: 2 góc kề bù có tổng số đo là 180 độ.
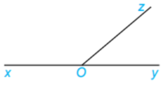
Góc xOz và góc yOz là 2 góc kề bù vì có tia Oz chung; tia Ox và Oy là 2 tia đối nhau.
Ta có: \(\widehat {xOz} + \widehat {yOz} = {180^0}\)
Nếu điểm M nằm trong góc xOy thì ta nói tia OM nằm giữa 2 tia Ox và Oy. Khi đó:
\(\widehat {xOM} + \widehat {MOy} = \widehat {xOy}\)
II. Hai góc đối đỉnh
2 góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Ví dụ: Trong hình vẽ dưới đây thì \(\widehat {AOC}\) và \(\widehat {BOD}\) là hai góc đối đỉnh.
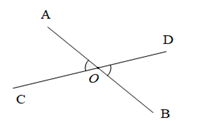
Tính chất: Hai góc đối đỉnh thì bằng nhau
Chú ý:
+ 2 đường thẳng cắt nhau tạo thành 2 cặp góc đối đỉnh
+ 2 đường thẳng cắt nhau và trong các góc tạo thành có một góc vuông thì 2 đường thẳng đó vuông góc.
Ví dụ: \(\widehat {AOC}\) và \(\widehat {BOD}\) là hai góc đối đỉnh thì \(\widehat {AOC} = \widehat {BOD}\).
III. Tia phân giác của một góc
Tia nằm giữa 2 cạnh của một góc và tạo với 2 cạnh ấy hai góc bằng nhau được gọi là tia phân giác của góc đó.
Tính chất: Khi Oz là tia phân giác của góc xOy thì \(\widehat {xOz} = \widehat {zOy} = \dfrac{1}{2}\widehat {xOy}\).
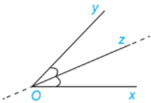
Chú ý: Đường thẳng chứa tia phân giác của một góc là đường phân giác của góc đó.

