I. Tam giác cân
Tam giác cân là tam giác có hai cạnh bằng nhau.
Ví dụ: \(\Delta ABC\) cân tại A \( \Leftrightarrow AB = AC\)
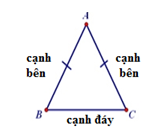
II. Tính chất tam giác cân
Trong tam giác cân, hai góc ở đáy bằng nhau. Ngược lại một tam giác có hai góc ở đáy bằng nhau thì đó là tam giác cân.
Chú ý:
+ Tam giác đều là tam giác có ba cạnh bằng nhau
+ Tam giác vuông cân là tam giác vuông và cân.
Ví dụ: \(\Delta ABC\) đều \( \Leftrightarrow AB = BC = CA\)
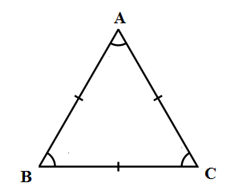
Nhận xét:
+ Tam giác cân có một góc bằng \({60^o}\) là tam giác đều
+ Tam giác cân có một góc ở đáy bằng \({45^o}\) là tam giác vuông cân.
III. Định nghĩa đường trung trực của một đoạn thẳng
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
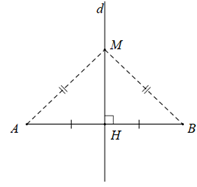
Hình vẽ trên, $d$ là đường trung trực của đoạn thẳng $AB.$
IV. Tính chất đường trung trực của một đoạn thẳng
+ Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
+ Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Ta có:
+ $M$ thuộc đường trung trực của $AB$\(\Rightarrow\) $MA = MB.$
+$MA = MB$ \(\Rightarrow\) M thuộc đường trung trực của $AB.$
Nhận xét:
Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.

