Trong công thức liên hệ giữa quãng đường đi được, vận tốc và gia tốc của chuyển động nhanh dần đều \({v^2} - v_0^2 = 2{\rm{as}}\), ta có các điều kiện nào sau đây?
Công thức \({v^2} - v_0^2 = 2{\rm{as}}\) chỉ đúng khi chuyển động là không đổi chiều. Với v > v0 => vật chuyển động theo chiều dương, chuyển động là nhanh dần nên a và v cùng chiều do vậy a > 0, quãng đường s là một đại lượng không âm
Cho đồ thị v - t của hai ôtô như hình vẽ:
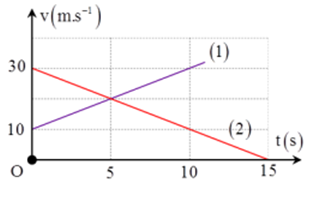
Chọn phương án đúng?
Từ đồ thị ta suy ra,
+ Phương trình vận tốc của oto 1 là: \({v_1} = 10 + 2t\)
+ phương trình vận tốc của oto 2 là: \({v_2} = 30 - 2t\)
Một chất điểm chuyển động thẳng có đồ thị vận tốc - thời gian như hình vẽ. Trong suốt quá trình chuyển động, tốc độ trung bình là 9 m/s. Phương trình chuyển động của chất điểm khi đi từ B đến C là?
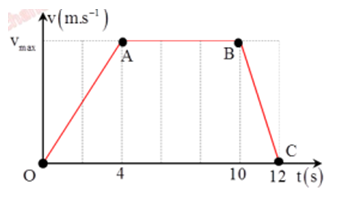
Ta có :
+ Tốc độ trung bình của vật : \({v_{tb}} = \dfrac{s}{t} = \dfrac{{\dfrac{1}{2}{v_{{\rm{max}}}}.4 + {v_{{\rm{max}}}}.6 + \dfrac{1}{2}{v_{{\rm{max}}}}.2}}{{12}} = 9 \to {v_{{\rm{max}}}} = 12m/s\)
+ Gia tốc của chất điểm khi chuyển động từ B đến C: \(a = \dfrac{{0 - 12}}{2} = - 6m/s\)
=> Phương trình chuyển động của chất điểm khi đi từ B đến C là: \(x = 96 + 12(t - 10) - 3{(t - 10)^2}\)
Hai người đi xe đạp khởi hành cùng một lúc từ 2 địa điểm A và B, đi ngược chiều nhau. Người đi từ A có vận tốc đầu là \(18km/h\) và chuyển động chậm dần đều với gia tốc \(20cm/{s^2}\). Người đi từ B có vận tốc đầu là \(5,4m/s\) và chuyển động nhanh dần đều với gia tốc\(0,2m/{s^2}\). Khoảng cách giữa hai người lúc đầu là \(130m\). Hỏi sau bao lâu 2 người gặp nhau và vị trí gặp nhau?
Chọn gốc tọa độ tại A, chiều dương là chiều từ A đến B, gốc thời gian là lúc hai người bắt đầu khởi hành.
Xe xuất phát từ A có:
\(\left\{ \begin{array}{l}{x_A} = 18km/h = 5m/s\\{a_A} = - 20cm/{s^2} = - 0,2m/{s^2}\\{x_{0A}} = 0\end{array} \right. \Rightarrow {x_A} = 5t - 0,1{t^2}\,\left( m \right)\)
Xe xuất phát từ B có:
\(\left\{ \begin{array}{l}{x_B} = - 5,4m/s\\{a_B} = - 0,2m/{s^2}\\{x_{0B}} = 130m\end{array} \right. \Rightarrow {x_B} = 130 - 5,4t - 0,1{t^2}\,\left( m \right)\)
Hai xe gặp nhau khi:
\(\begin{array}{l}{x_A} = {x_B} \Leftrightarrow 5t - 0,1{t^2} = 130 - 5,4t - 0,1{t^2}\\ \Rightarrow t = 12,5s\end{array}\)
Thay \(t = 12,5s\) vào phương trình của \({x_A}\) ta được:
\({x_A} = 5.12,5 - 0,1.12,{5^2} = 46,875m\)
Một vật chuyển động có đồ thị vận tốc như hình bên. Công thức vận tốc và công thức đường đi của vật là:
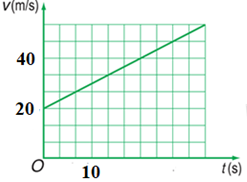
Biễu diễn số liệu như hình vẽ:
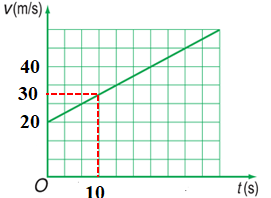
Từ đồ thị ta có: \(\left\{ \begin{array}{l}{t_0} = 0;{v_0} = 20m/s\\{t_1} = 10s;{v_1} = 30m/s\end{array} \right.\)
Gia tốc của vật: \(a = \dfrac{{{v_1} - {v_0}}}{{{t_1} - {t_0}}} = \dfrac{{30 - 20}}{{10}} = 1m/{s^2}\)
Công thức vận tốc và quãng đường:
\(\left\{ \begin{array}{l}v = {v_0} + at = 20 + 1.t\\s = {v_0}t + \dfrac{1}{2}a{t^2} = 20.t + \dfrac{1}{2}.1.{t^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}v = 20 + t\,\,\left( {m/s} \right)\\s = 20t + \dfrac{{{t^2}}}{2}\,\left( m \right)\end{array} \right.\)

