Một chiếc xe nặng 500kg đang chuyển động thẳng đều thì hãm phanh để xe chuyển động chậm dần đều. Biết trong giây cuối cùng xe đi được 1m. Độ lớn lực hãm phanh bằng:
Quãng đường vật đi trong 1s cuối là: \(\Delta S = {S_t} - {S_{t - 1}}\)
\(\begin{array}{l} \Rightarrow 1 = {v_0}t + \dfrac{1}{2}a{t^2} - \left[ {{v_0}\left( {t - 1} \right) + \dfrac{1}{2}a{{\left( {t - 1} \right)}^2}} \right]\\ \Leftrightarrow 1 = {v_0}t + \dfrac{1}{2}a{t^2} - {v_0}t + {v_0} - \dfrac{1}{2}a{t^2} + at - \dfrac{1}{2}a\\ \Leftrightarrow 1 = {v_0} + at - \dfrac{a}{2}\left( 1 \right)\end{array}\)
mặt khác có: \(a = \dfrac{{v - {v_0}}}{t} = \dfrac{{ - {v_0}}}{t}\left( 2 \right)\)
từ (1) và (2) ta có: \( - at + at - \dfrac{a}{2} = 2 \Rightarrow a = - 2m/s\)
do lực tac dụng là lực hãm nên ngược chiều chuyển động
Áp dụng biểu thức định luật II Newton: \( - {F_h} = ma \Rightarrow {F_h} = 500.2 = 1000N\)
Một vật có trọng lượng P đứng cân bằng nhờ 2 dây OA làm với trần một góc 600 và OB nằm ngang. Độ lớn lực căng T1 của dây OA bằng:
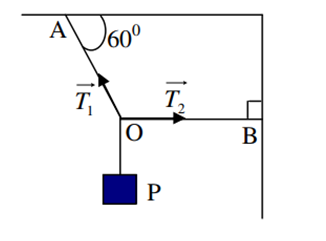
+ Phân tích lực \({\overrightarrow T _1}\) thành hai thành phần theo phương Ox và Oy, ta có:
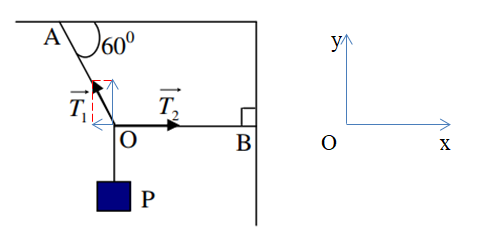
Vật cân bằng => Tổng tất cả các lực tác dụng lên vật bằng 0
Từ hình ta có:
Theo phương Oy: \({T_1}\sin {60^0} = P \to {T_1} = \frac{P}{{\sin {{60}^0}}} = \frac{{2P}}{{\sqrt 3 }}\)
Cho viên bi $A$ chuyển động tới va chạm vào bi $B$ đang đứng yên, ${v_A} = {\rm{ }}2m/s$ sau va chạm bi $A$ tiếp tục chuyển động theo phương cũ với $v = 1m/s$, thời gian xảy ra va chạm là $0,4s$. Tính gia tốc của viên bi thứ $2$ , biết ${m_A} = {\rm{ }}200g,{\rm{ }}{m_B} = {\rm{ }}100g$.
Ta xét chuyển động của xe $A$ có vận tốc trước khi va chạm là \({v_A} = 2m/s\), sau va chạm xe A có vận tốc là \(v = 1m/s\)
Áp dụng biểu thức xác định gia tốc: \(a = \dfrac{{{v_2} - {v_1}}}{{\Delta t}} = \dfrac{{1 - 2}}{{0,4}} = - 2,5m/s\)
+ Theo định luật $III$ Niu-tơn: \({\overrightarrow F _{AB}} = - {\overrightarrow F _{BA}}\)
+ Theo định luật $II$, ta có: $F = ma$
\(\begin{array}{l} \to {|F_{AB}|} = {|F_{BA}|} \leftrightarrow {m_A}{|a_A|} = {m_B}{a_B}\\ \to {a_B} = \dfrac{{{m_A}{|a_A|}}}{{{m_B}}} = \dfrac{{0,2.2,5}}{{0,1}} = 5m/{s^2}\end{array}\)
Một người có trọng lượng 500N đứng trên mặt đất. Lực mà mặt đất tác dụng lên người đó có độ lớn là :
Từ định luật III Newton ta có: lực đất tác dụng lên người bằng với trọng lượng của người tác dụng lên đất
nên ta có lực mà mặt đất tác dụng lên người đó có độ lớn là bằng 500N
Một vật có khối lượng $4kg$, dưới tác dụng của lực F thu được gia tốc $3m/{s^2}$. Đặt thêm vào vật một vật khác thì cũng lực ấy chỉ gây được gia tốc $2 m/{s^2}$. Khối lượng của vật đặt thêm vào là:
Theo định luật II - Niutơn, ta có: \(F = ma\)
+ Khi \(m = {m_1} = 4kg\) thì \({a_1} = 3m/{s^2}\)
+ Khi \(m = {m_2}\) thì \({a_2} = 2m/{s^2}\)
Ta có, lực trong hai trường hợp là như nhau:
\(\begin{array}{l} \leftrightarrow {m_1}{a_1} = {m_2}{a_2} \leftrightarrow 4.3 = {m_2}.2\\ \to {m_2} = 6kg\end{array}\)
=> Khối lượng vật thêm vào là: \(6 - 4 = 2kg\)

