Bài 11. Phương thức con người khai thác, sử dụng và bảo vệ thiên nhiên châu Phi
Sách chân trời sáng tạo
Khó khăn trong việc bảo vệ thiên nhiên của châu Phi là
Châu Phi nổi tiếng với sự đa dạng các loài động vật hoang dã. Tuy nhiên, nạn săn trộm, mua bán bất hợp pháp các sản phẩm như ngà voi, sừng tê giác,...làm cho số lượng các loài động vật hoang dã suy giảm đáng kể. Đây là vấn đề nan giải của châu Phi trong công cuộc bảo vệ thiên nhiên.
Cho cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 3\) và công sai \(d = 7\). Hỏi kể từ số hạng thứ mấy trở đi thì các số hạng của \(\left( {{u_n}} \right)\) đều lớn hơn 2018 ?
Ta có: \({u_n} = {u_1} + \left( {n - 1} \right)d = 3 + \left( {n - 1} \right).7\) \( = 7n - 4\)
Các số hạng của \(\left( {{u_n}} \right)\) đều lớn hơn 2018 khi \(7n - 4 > 2018 \Leftrightarrow n > \dfrac{{2022}}{7} \approx 288,86\)
Vậy n=289
Đồ thị nào của hàm số dưới đây có tiệm cận ngang?
Ta có: \(\mathop {\lim }\limits_{x \to \infty } \dfrac{{3{x^2} + 2x - 1}}{{4{x^2} + 5}} = \dfrac{3}{4} \Rightarrow y = \dfrac{3}{4}\) là tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{3{x^2} + 2x - 1}}{{4{x^2} + 5}}\).
Tìm tham số \(m\) để hàm số \(y = \sqrt {2{{\sin }^2}x + \sqrt 3 \sin 2x + m} \) có tập xác định \(D = \mathbb{R}\).
Hàm xác định trên \(\mathbb{R}\) khi và chỉ khi:
\(\begin{array}{l}2{\sin ^2}x + \sqrt 3 \sin 2x + m \ge 0\forall x\\ \Leftrightarrow - m \le 2{\sin ^2}x + \sqrt 3 \sin 2x\\ \Leftrightarrow - m \le \min \left( {2{{\sin }^2}x + \sqrt 3 \sin 2x} \right)\end{array}\)
Ta có:
\(\begin{array}{l}2{\sin ^2}x + \sqrt 3 \sin 2x\\ = 1 - \cos 2x + \sqrt 3 \sin 2x\\ = 1 + 2\left( {\dfrac{{\sqrt 3 }}{2}\sin 2x - \dfrac{1}{2}\cos s2x} \right)\\ = 1 + 2\sin \left( {2x - \dfrac{\pi }{6}} \right) \ge 1 + 2.\left( { - 1} \right) = - 1\end{array}\)
$=>-m\le -1$
Vậy \(m \ge 1\)
Cho hàm số \(f(x)\) thoả mãn \(\int_0^e {{f^\prime }} (x)dx = 1,f(0) = e\). Tính \(f(e)\)
Ta có: \(\int_0^e {{f^\prime }} (x)dx = 1 = f\left( e \right) - f\left( 1 \right) = f\left( e \right) - e\) \( \Rightarrow f\left( e \right) = 1 + e\)
Trong không gian hệ tọa độ $O x y z$, cho \(A(1;2; - 1);B( - 1;0;1)\) và mặt phẳng \((P):x + 2y - z + 1 = 0\). Viết phương trình mặt phẳng \((Q)\) qua $A, B$ và vuông góc với \((P)\).
Ta có: \(\overrightarrow {AB} = \left( { - 2;{\mkern 1mu} {\mkern 1mu} - 2;{\mkern 1mu} 2} \right);{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \overrightarrow {{n_P}} = \left( {1;{\mkern 1mu} 2;{\mkern 1mu} {\mkern 1mu} - 1} \right)\)
\( \Rightarrow \overrightarrow {{n_Q}} = \left[ {\overrightarrow {AB} ;{\mkern 1mu} {\mkern 1mu} \overrightarrow {{n_P}} } \right]\)\( = \left( { - 2;0; - 2} \right)\)
Phương trình mặt phẳng (Q) đi qua \(A\left( {1;{\mkern 1mu} 2; - 1} \right)\) và có VTPT \(\overrightarrow {{n_Q}} = \left( {1;0;1} \right)\) là:
\(1\left( {x - 1} \right) + 0\left( {y - 2} \right) + 1\left( {z + 1} \right) = 0\)\( \Leftrightarrow x + z = 0\)
Từ một miếng tôn có hình dạng là nửa đường tròn bán kính \(1\;{\rm{m}}\), người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu?


Xét đường tròn bán kính 1, ta cắt trên đó một hình chữ nhật ABCD.
Khi đó \({S_{ABCD}} = \dfrac{1}{2}AC.BD.\sin a\) \( = 2\sin \alpha \le 2\)
Dấu bằng xảy ra khi và chỉ khi \(\alpha = {90^0}\)
Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng 1.
Một vật chuyển động với vận tốc \(v(t) = 3{t^2} + 4(\;{\rm{m}}/{\rm{s}})\), trong đó \(t\) là khoảng thời gian tính bằng giây. Tính quãng đường vật đó đi được trong khoảng thời gian từ giây thứ 3 đến giây thứ 10?
Ta có: \(v\left( t \right) = 3t^2 + 4\,\,\left( {m/s} \right)\)
Khi đó quãng đường của vật được tính từ giây thứ 3 đến giây thứ 10 là:
\(s\left( t \right) = \int\limits_3^{10} {\left( {3t^2+ 4} \right)dt} \) \( = 1001\,\,(m).\)
Cho hai mặt phẳng \((P),(Q)\) song song với nhau cùng cắt khối cầu tâm \(I\), bán kính \(R\) tạo thành hai hình tròn cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn, đáy trùng với hình tròn còn lại. Tính khoảng cách giữa \((P),(Q)\) để diện tích xung quanh của hình nón là lớn nhất.
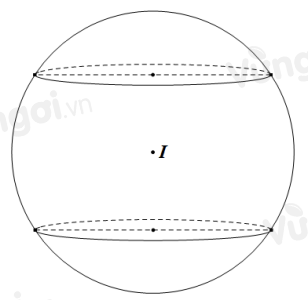
Cắt khối cầu tâm I, bán kính R bằng mặt phẳng (R) đi qua tâm I và vuông góc với hai mặt phẳng (P) và (Q) ta được hình vẽ sau:

Trong đó \(AB = \left( R \right) \cap \left( P \right),CD = \left( R \right) \cap \left( Q \right)\) với \(AB = CD;\) \(h = SH = AC = BD,R = IB\)
Đường sinh \(l = SC = SD\)
Bán kính của mỗi hình tròn giao tuyến là \(r = \dfrac{{AB}}{2}\)
Ta có: \({l^2} = S{C^2} = A{C^2} + A{S^2} = {h^2} + {r^2}\)
\( \Rightarrow {l^2} = {R^2} + \dfrac{{{h^2}}}{4}\)
Mà diện tích xung quanh của khối nón được xét: \({S_{xq}} = \pi rl\)
Ta có \({S_{xq}}\) đạt giá trị lớn nhất khi và chỉ khi \(rl\) đạt giá trị lớn nhất.
Áp dụng bất đẳng thức Cauchy cho 2 số \(r\sqrt 3 \) và \(l\) ta có
\(rl = \dfrac{1}{{2\sqrt 3 }}.2.\left( {r\sqrt 3 } \right)l \le \dfrac{{\sqrt 3 }}{6}\left( {3{r^2} + {l^2}} \right)\) \( = \dfrac{{\sqrt 3 }}{6}4{R^2} = \dfrac{{2{R^2}\sqrt 3 }}{3}\)
=> \(rl\) đạt giá trị lớn nhất khi và chỉ khi \(3{r^2} = {l^2} \Leftrightarrow {h^2} = \dfrac{4}{3}{R^2} \Rightarrow h = \dfrac{{2R\sqrt 3 }}{3}\)
Biết rằng tập nghiệm của bất phương trình \(\left( {{{\log }_2}(4x) - 4} \right)\left( {{{\log }_2}x - m} \right) < 0\) chứa đúng 1000 số nguyên. Mệnh đề nào dưới đây đúng?
Điều kiện: \(x > 0\)
\(\left[ {{{\log }_2}(4x) - 4} \right]\left( {{{\log }_2}x - m} \right) < 0\)\( \Leftrightarrow \left( {{{\log }_2}x - 2} \right)\left( {{{\log }_2}x - m} \right) < 0\)(*)
TH1: Nếu \(m = 2\)(*) \( \Leftrightarrow {\left( {{{\log }_2}x - 2} \right)^2} < 0 \Rightarrow \left( * \right)\) vô nghiệm (Loại)
TH2: Nếu \(m < 2\left( * \right) \Leftrightarrow m < {\log _2}x < 2 \Leftrightarrow {2^m} < x < 4\)m<2
=> Tập nghiệm của BPT là \(S = \left( {{2^m};4} \right)\) chứa tối đa 3 số nguyên: 1;2;3(Loại)
TH3: Nếu \(m > 2 \Rightarrow \)\(\left( * \right) \Leftrightarrow 2 < {\log _2}x < m \Leftrightarrow 4 < x < {2^m}\)
=> Tập nghiệm của BPT là \(S = \left( {4;{2^m}} \right)\)
\(\begin{array}{l} \Rightarrow 5 \le x \le {2^m} - 1\\{2^m} - 1 - 5 + 1 = {2^m} - 5\end{array}\)
Theo giả thiết ta có: \({2^m} - 5 = 1000 \Leftrightarrow m = {\log _2}1005 \approx 9,97\)

