Đề bài
Chứng tỏ rằng (4.1) cũng đúng cả trong trường hợp q < 0
Lời giải chi tiết
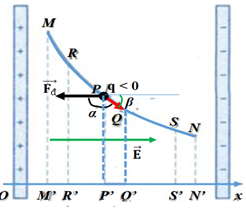
Khi một điện tích q < 0 di chuyển từ M đến N trong một điện trường đều có cường độ điện trường E, lực điện trường \(\overrightarrow F \) sẽ có chiều như hình vẽ, công của lực điện trường được tính bởi công thức:
\({A_{MN}} = \sum {\Delta A = \Delta {A_{M{\rm{R}}}} + \Delta {A_{RP}} + \Delta {A_{PQ}} + ...\\ + \Delta {A_{S'N'}}} \)
Trong đó:
\(\begin{array}{l}\Delta {A_{PQ}} = \overrightarrow F .\overrightarrow {PQ} = F.PQ.\cos \alpha \\ \Rightarrow \Delta {A_{PQ}} = {F_d}.PQ.\cos \left( {{{180}^0} - \beta } \right) \\= \left( { - qE} \right).PQ.\left( { - \cos \beta } \right)\\ = qE.\overline {P'Q'} \end{array}\)
Với \(\alpha = \left( {\overrightarrow {{F_d}} ,\overrightarrow {PQ} } \right)\)
Tương tự:
\(\Delta {A_{MR}} = q.E.\overline {M'R} ;\Delta {A_{RP}} = q.E.\overline {R'P'} \)
\(\Delta {A_{S'N'}} = q.E.\overline {S'N'} \)
Công của lực điện trường trên quãng đường MN bằng:
\(\begin{array}{l}{A_{MN}} = q.E.\left( {\overline {M'R'} + \overline {R'P'} + \overline {P'Q'} + ... + \overline {S'N'} } \right)\\ \Rightarrow {A_{MN}} = q.E.\overline {M'N'} \end{array}\)
=> đpcm