Đề bài
Một cái chậu đặt trên một mặt phẳng nằm ngang, chứa một lớp nước dày 20 cm, chiết suất \(n = {4 \over 3}\). Đáy chậu là một gương phẳng. Mặt M cách mặt nước 30 cm, nhìn thẳng góc xuống đáy chậu. Xác định khoảng cách từ ảnh của mắt tới mặt nước. Vẽ đường đi của ánh sáng qua quang hệ trên.
Lời giải chi tiết
Để giải bài toán này, trước hết ta tìm công thức xác định vật và ảnh của hệ hai môi trường trong suốt (thường là một lưỡng chất phẳng). Ta xét chùm tia sáng hẹp gần như vuông góc với mặt lưỡng chất.
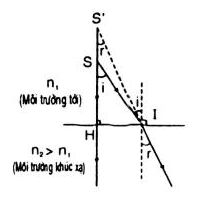
Ta có: \(\tan i = {{IH} \over {SH}} \approx \sin i\) (vì là góc nhỏ)
\({\mathop{\rm t}\nolimits} {\rm{anr}} = {{IH} \over {S'H}} \approx {\mathop{\rm s}\nolimits} {\rm{inr}}\) (vì là góc nhỏ)
\( \Rightarrow {{\sin i} \over {\sin \,r}} = {{S'H} \over {SH}} = {{{n_2}} \over {{n_1}}}\)
Suy ra \({{S'H} \over {{n_2}}} = {{SH} \over {{n_1}}}\) (Công thức này đúng cho mọi trường hợp)
Trở lại bài toán, ta có hình vẽ sau:
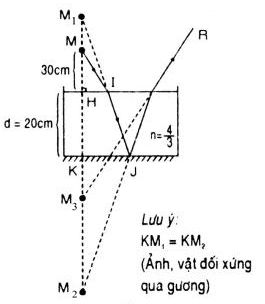
Xét trường hợp ánh sáng đi từ không khí (n1=1) vào nước (\({n_2} = {4 \over 3}\))
Theo công thức trên:\({{{M_1}H} \over {{n_2}}} = {{MH} \over {{n_1}}}\)
\( \Rightarrow {{MH} \over 1} = {{{M_1}H} \over {{4 \over 3}}}\)
\( \Rightarrow {M_1}H = {4 \over 3}MH = {4 \over 3}.30 = 40\,cm\)
Gọi M2 là ảnh ảo của mắt M qua gương phẳng đáy chậu, ta có M2 đối xứng với M1 qua gương:
\(K{M_2} = K{M_1} = KH + H{M_1} = 20+40=60\left( {cm} \right)\)
Xét trường hơp tia sáng phản xa đi từ nước ( \({n_1} = {4 \over 3}\)) ra không khí
(n2 = 1), ta có M3 là ảnh của M2, M3 là ảnh của mắt mà mắt thấy được.
Theo công thức trên:
\({{H{M_3}} \over {{n_2}}} = {{H{M_2}} \over {{n_1}}} \Rightarrow {{H{M_3}} \over 1} = {{H{M_2}} \over {{4 \over 3}}} = {3 \over 4}\left( {H{M_2}} \right) \\= {3 \over 4}\left( {HK + K{M_2}} \right)\)
\(\; \Rightarrow {\rm{ }}H{M_3} = {3 \over 4}(20 + {\rm{ }}60){\rm{ }} = {\rm{ }}60{\rm{ }}\left( {cm} \right)\)
Vậy khoảng cách từ ảnh M3 đến mặt nước là 60 (cm)

