Đề bài
Từ công thức (10.4) \(I = \frac{{\xi - {U_{AB}}}}{{R + r}}\)
và (14.1) \({U_{AB}} = {V_A} - {V_B} = \xi - r.I\). Hãy chứng minh 14.3 :
\({U_{AB}} = {V_A} - {V_B} = \xi - \left( {R + r} \right).I\)
Lời giải chi tiết
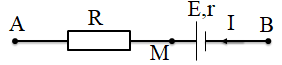
Ta có \({U_{BA}} = {U_{BM}} + {U_{MA}}\)
\({U_{BA}} = rI - \xi + RI\)
\( \Rightarrow {U_{AB}} + \xi = \left( {r + R} \right)I \Rightarrow I = {{{U_{BA}} + \xi } \over {R + r}}\)