Đề bài
Chọn phương án dứng.
Một tia sáng tới vuông góc với mặt AB của một lăng kính có chiết suất \(n = \sqrt 2 \) và góc ở đỉnh A = 30°, B là góc vuông. Góc lệch của tia sáng qua lăng kính là:
A. 5° B. 13°
C. 15° D. 22°
Lời giải chi tiết
C là phương án đúng
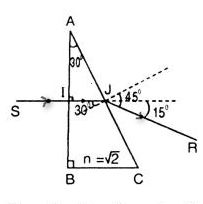
Ta có: \(i = {30^0} \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{{n_1}\sin i} \over {{n_2}}}\)
\( \Rightarrow \sin r = {{\sqrt 2 \sin {{30}^0}} \over 1} = {{\sqrt 2 } \over 2} \Rightarrow r = {45^0}\)
Góc lệch D = 45° - 30° = 15°

