Đề bài
Một bản mặt song song (một bản trong suốt giới hạn bởi hai mặt pỉiẳng song song) có bể dày 10cm, chiết suất n = 1,5 được đặt trong không khí. Chiếu tới bản một tia sáng SI có góc tới là 45°.
a) Chứng tỏ ràng tia sáng ló ra khỏi bân có phương song song với tia tới. Vẽ đường đi của tia sáng qua bản.
b) Tính khoảng cách giữa giá của tia ló và tia tới.
Lời giải chi tiết
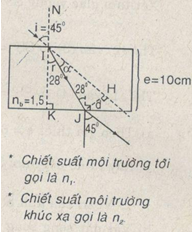
a) Không khí (n1) —> bản song song (n2):
Trước hết tia sáng đi từ không khí vào bản song song; ta có khúc xạ cụp, vì nkk< nb
Theo định luật khúc xạ ánh sáng
\({n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}} \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{{n_1}\sin i} \over {{n_2}}}\)
Thay số: \({\mathop{\rm s}\nolimits} {\rm{inr = }}{{1\sin {{45}^0}} \over {1,5}} = 0,47 \Rightarrow r = {28^0}\)
Bản song song -> không khí:
Theo tínn truyền thuận nghịch của tia sáng, ta có góc tới i = 28° thì góc khúc xạ là r = 45° nên tia ló ra khỏi bản sẽ song song với tia tới.
b) Gọi d là khoảng cách giữa giá của tia tới và tia ló, d = JH.
Xét tam giác vuông IKJ:
\({\rm{cos\,r = }}{{IK} \over {IJ}} \Rightarrow {\rm{I}}J = {{IK} \over {{\rm{cos\,r}}}} = {e \over {{\rm{cos\,r}}}}\)
Xét tam giác vuông IHJ:
\(\sin \alpha = sin\left( {i - r} \right) = {{JH} \over {IJ}} \Rightarrow JH = IJsin\left( {i - r} \right)\)
\( \Rightarrow d = {e \over {{\rm{cos\,r}}}}\sin \left( {i - r} \right)\)
(công thức tính khoảng cách giữa giá của tia ló là tia tới của bản song song).
Thay số:
\(d = {{10} \over {{\rm{cos2}}{{\rm{8}}^0}}}\sin \left( {{{45}^0} - {{28}^0}} \right) = 3,3\left( {cm} \right)\)

