Bài tập chuyển động đều - Chuyển động không đều

Vận tốc trung bình của Hưng trên cả đoạn đường:

${v_{tb}} = \dfrac{S}{t} = \dfrac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}} = \dfrac{{{S_1} + {S_2}}}{{\dfrac{{{S_1}}}{{{v_1}}} + {t_2}}} = \dfrac{{100 + 140}}{{\dfrac{{100}}{2} + 30}} = 3m/s$

Quãng đường người xe đạp đi được trong 1 giờ là:

$S = {v_{tb}}t = 10.1 = 10km = 10\,000m$

Ta có:  $S = v.t \Rightarrow t = \frac{S}{v} = \frac{{200}}{4} = 50\left( s \right)$

Cách giải:

Vận tốc trong ½ thời gian đầu là 30km/h:

${v_1} = \frac{{{S_1}}}{{{t_1}}} = \frac{{{S_1}}}{{\frac{t}{2}}} = \frac{{2{S_1}}}{t} \Rightarrow {S_1} = \frac{{{v_1}t}}{2} = \frac{{30.t}}{2} = 15t\,\,\,\left( {km} \right)$

Vận tốc trong ½ thời gian sau là 15m/s = 54km/h:

${v_2} = \frac{{{S_2}}}{{{t_2}}} = \frac{{{S_2}}}{{\frac{t}{2}}} = \frac{{2{S_2}}}{t} \Rightarrow {S_2} = \frac{{{v_2}t}}{2} = \frac{{54.t}}{2} = 27t\,\,\,\left( {km} \right)$

→ Tổng quãng đường: $S = {S_1} + {S_2} = 15t + 27t = 42t\,\,\left( {km} \right)$

→ Vận tốc trung bình trên cả đoạn đường: ${v_{tb}} = \frac{S}{t} = \frac{{42t}}{t} = 42\,\,\left( {km/h} \right)$

Thời gian xe máy đi trên 3 quãng đường lần lượt là:

$\begin{array}{l} {t_1} = \frac{{{S_1}}}{{{v_1}}} = \frac{4}{{48}} = \frac{1}{{12}}\,\,\left( h \right)\\ {t_2} = \frac{{{S_2}}}{{{v_2}}} = \frac{2}{{36}} = \frac{1}{{18}}\,\,\left( h \right)\\ {t_3} = \frac{{{S_3}}}{{{v_3}}} = \frac{5}{{45}} = \frac{1}{9}\,\,\left( h \right) \end{array}$

Tổng thời gian xe máy đi hết toàn bộ quãng đường là:

$t = {t_1} + {t_2} + {t_3} = \frac{1}{{12}} + \frac{1}{{18}} + \frac{1}{9} = \frac{1}{4}\,\,\left( h \right)$

Vận tốc trung bình của xe máy trên cả đoạn đường là:

${v_{tb}} = \frac{{{S_1} + {S_2} + {S_3}}}{t} = \frac{{4 + 2 + 5}}{{\frac{1}{4}}} = 44\,\,\left( {km/h} \right)$

Thời điểm và vị trí hai xe cách nhau $30km$:

Từ thời điểm $t = 2,5h$  kẻ đường thẳng song song với trục tung cắt hai đồ thị tại hai điểm $I$ và $K$, tung độ của $I$ là ${x_2} = 20km$ , của K là ${x_1} = 50km$.

Vậy hai xe cách nhau  $l = {x_1} - {x_2} = 50 - 20 = 30km$

Xét tương tự với thời điểm $t = 3,5h$, ta cũng có hai xe cách nhau $30km$

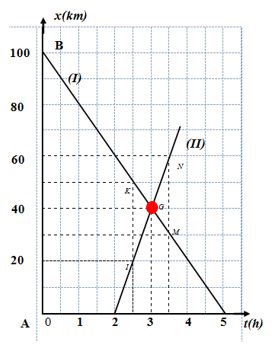
Tọa độ giao điểm của hai đồ thị cho biết:

- Hai xe gặp nhau sau $3h$ kể từ khi xe (I) khởi hành từ $B$, sau $1h$ kể từ khi xe (II) khởi hành từ $A$

- Vị trí gặp cách $A$: $40km$.

Từ đồ thị, ta thấy hai xe xuất phát từ các thời điểm khác nhau

Xe (I) xuất phát trước xe (II) 2 giờ

Từ đồ thị, ta thấy hai xe xuất phát từ các thời điểm khác nhau

Xe (I) xuất phát trước xe (II) 2 giờ

Gọi vận tốc của canô khi dòng nước không chảy là: ${V_{can{\rm{o}}}}$

Vận tốc của canô + vận tốc dòng chảy bằng: $\dfrac{{AB}}{t} = \dfrac{{30}}{2} = 15km/h$

Ta có:

Khi canô xuôi dòng: ${V_{can{\rm{o}}}} + 3 = 15$

$\to {V_{can{\rm{o}}}} = 12km/h$

Khi ngược dòng, thời gian canô phải đi là:

$t = \dfrac{{30}}{{12 - 3}} = \dfrac{{10}}{3}h = 200p = 3h20p$

Gọi ${v_1},{v_2}$ lần lượt là vận tốc mà người đó đi nửa đoạn đường đầu và nửa đoạn đường sau.

${t_1},{t_2}$ lần lượt là thời gian mà người đó đi nửa đoạn đường đầu và nửa đoạn đường sau.

Ta có:

${v_{tb}} = \dfrac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \dfrac{{2{\rm{s}}}}{{{t_1} + {t_2}}}{\rm{          }}\left( 1 \right)$

Mặt khác, ta có: $\left\{ \begin{array}{l}{t_1} = \dfrac{s}{{{v_1}}}\\{t_2} = \dfrac{s}{{{v_2}}}\end{array} \right.$

Thay vào $\left( 1 \right)$ ta được: 

$\begin{array}{l}{v_{tb}} = \dfrac{{2{\rm{s}}}}{{\dfrac{s}{{{v_1}}} + \dfrac{s}{{{v_2}}}}}\\ \leftrightarrow 8 = \dfrac{2}{{\dfrac{1}{{{v_1}}} + \dfrac{1}{{12}}}}\\ \to {v_1} = 6km/h\end{array}$

Gọi ${v_1},{v_2}$ lần lượt là vận tốc của ô tô trên hai nửa quãng đường

${t_1},{t_2}$ lần lượt là thời gian của ô tô trên hai nửa quãng đường

Ta có:

${v_{tb}} = \dfrac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \dfrac{{2{\rm{s}}}}{{{t_1} + {t_2}}}{\rm{          }}\left( 1 \right)$

Mặt khác, ta có: $\left\{ \begin{array}{l}{t_1} = \dfrac{s}{{{v_1}}}\\{t_2} = \dfrac{s}{{{v_2}}}\end{array} \right.$

Thay vào $\left( 1 \right)$ ta được: 

$\begin{array}{l}{v_{tb}} = \dfrac{{2{\rm{s}}}}{{\dfrac{s}{{{v_1}}} + \dfrac{s}{{{v_2}}}}}\\ \leftrightarrow 40 = \dfrac{2}{{\dfrac{1}{{45}} + \dfrac{1}{{{v_2}}}}}\\ \to {v_2} = 36km/h\end{array}$

Ta có: $\left\{ \begin{array}{l}{t_1} = 30ph = 0,5h\\{t_2} = 15ph = 0.25h\end{array} \right.$

+ Quãng đường AB: $AB = {s_1} = {v_1}{t_1} = 10.0,5 = 5km$

+ Quãng đường BC: $BC = {s_2} = {v_2}{t_2} = 8.0,25 = 2km$

Vận tốc trung bình trên đoạn đường $ABC$ là :

${v_{tb}} = \dfrac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \dfrac{{5 + 2}}{{0,5 + 0,25}} = 9,3km/h$

Gọi quãng đường vật đi được trong $\dfrac{1}{3}$ thời gian đầu và $\dfrac{2}{3}$ thời gian sau lần lượt là: ${s_1},{s_2}$

Ta có: $\left\{ \begin{array}{l}{s_1} = {v_1}{t_1} = 12.\dfrac{t}{3} = 4t\\{s_2} = {v_2}{t_2} = 9.\dfrac{{2t}}{3} = 6t\end{array} \right.$

Vận tốc của ô tô trên cả đoạn đường:

${v_{tb}} = \dfrac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \dfrac{{4t + 6t}}{t} = 10m/s$

Vận tốc trung bình người đó là: ${v_{tb}} = \dfrac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}}$

Ta có,

+ Thời gian tàu chuyển động $81000m$  là: $t = 1,5.60.60 = 5400{\rm{s}}$

+ Vận tốc của tàu là: ${v_{tb}} = \dfrac{s}{t} = \dfrac{{81000}}{{5400}} = 15m/s$

${v_1} = 2m/s = 7,2km/h$

+ Thời gian người đó đi đoạn đường đầu là: ${t_1} = \dfrac{{{s_1}}}{{{v_1}}} = \dfrac{{3,6}}{{7,2}} = 0,5h$

+ Vận tốc trung bình của Hưng trên cả đoạn đường dốc là: ${v_{tb}} = \dfrac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \dfrac{{3,6 + 1,9}}{{0,5 + 0,3}} = 6,875km/h$

Ta có: ${v_{tb}} = \dfrac{s}{t} \to t = \dfrac{s}{{{v_{tb}}}} = \dfrac{{1,1}}{{4,4}} = 0,25h = 15$ phút.

${v_{tb}} = 10m/s = 36km/h$

Ta có: ${v_{tb}} = \dfrac{s}{t} \to s = {v_{tb}}t = 36.7,5 = 270km$

$15p = 0,25$ giờ

Ta có: ${v_{tb}} = \dfrac{s}{t} \to s = {v_{tb}}t = 8.0,25 = 2km$