I. Tính thể tích khối chóp có cạnh bên vuông góc với đáy
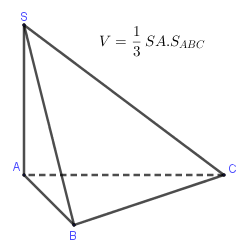
Cho khối chóp $S.ABC$ có cạnh bên $SA$ vuông góc với $(ABC)$
II. Tính thể tích khối chóp đều
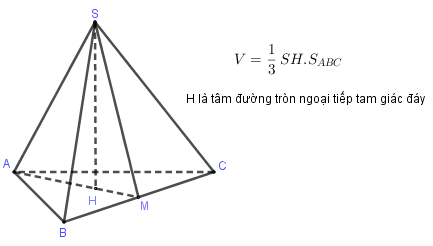
Hình chóp đều là hình chóp có đáy là đa giác đều và chân đường cao là tâm của đáy.
III. Định nghĩa và các phép toán vecto trong không gian
Định nghĩa: Vectơ trong không gian là một đoạn thẳng có hướng.
Kí hiệu: $\overrightarrow{AB}$ chỉ vectơ có điểm đầu là A và điểm cuối là B.
Các quy tắc:
Cho các véc tơ tùy ý \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) và \(k,l \in R\).
- Quy tắc ba điểm: Cho ba điểm \(A,B,C\) bất kì thì:
\(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \)
\(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \)
- Quy tắc hình bình hành: Cho hình bình hành \(ABCD\) ta có: \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \)
- Quy tắc hình hộp: Cho hình hộp \(ABCD.A'B'C'D'\) ta có \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
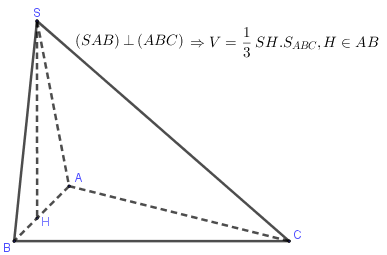
IV. Tính thể tích khối chóp có mặt bên vuông góc với đáy
V. Tính tỉ lệ thể tích các khối chóp.
Phương pháp:
- Bước 1: Chia các khối chóp cần tính tỉ lệ thể tích thành các khối chóp tam giác tương ứng với nhau.
- Bước 2: Áp dụng công thức tính tỉ số thể tích các khối chóp \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\), ở đó \(A' \in SA,B' \in SB,C' \in SC\)
Một số công thức tính thể tích khối tứ diện thường gặp trong đề thi
- Tứ diện đều cạnh \(a\): \(V = \dfrac{{{a^3}\sqrt 2 }}{{12}}\).
- Tứ diện vuông (các góc tại một đỉnh của tứ diện là góc vuông):
Tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc và \(AB = a,AC = b,AD = c\) ta có \(V = \dfrac{1}{6}abc\).
- Công thức tính thể tích sử dụng các độ dài, khoảng cách và góc giữa hai cạnh đối diện của tứ diện:
Tứ diện \(ABCD\) có \(AD = a,BC = b\), khi đó: \(V = \dfrac{1}{6}ab.\sin \left( {AD,BC} \right).d\left( {AD,BC} \right)\)
- Tứ diện gần đều (các cặp cạnh đối tương ứng bằng nhau):
Tứ diện \(ABCD\) có \(AB = CD = a;BC = AD = b;AC = BD = c\) ta có:
\(V = \dfrac{{\sqrt {2} }}{{12}}\sqrt {\left( {{a^2} + {b^2} - {c^2}} \right)\left( {{b^2} + {c^2} - {a^2}} \right)\left( {{a^2} + {c^2} - {b^2}} \right)} \)

