Nguyên hàm

I. Định nghĩa và tính chất

II. Bảng nguyên hàm

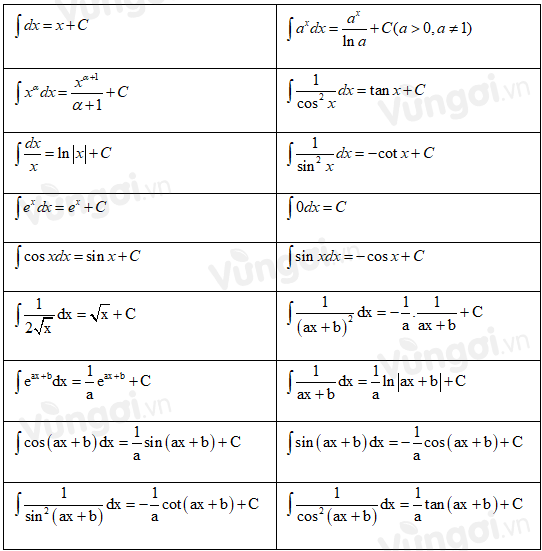
III. Tìm nguyên hàm của hàm số

Ví dụ: Tìm nguyên hàm của hàm số $f\left( x \right) = \dfrac{{{{\left( {{x^2} - 1} \right)}^2}}}{{{x^2}}}$.

Giải:

Ta có: $f\left( x \right) = \dfrac{{{{\left( {{x^2} - 1} \right)}^2}}}{{{x^2}}} = \dfrac{{{x^4} - 2{x^2} + 1}}{{{x^2}}}$ $= {x^2} - 2 + \dfrac{1}{{{x^2}}}$

Do đó $F\left( x \right) = \int {\left( {{x^2} - 2 + \dfrac{1}{{{x^2}}}} \right)dx}$ $= \int {{x^2}dx}  - 2\int {dx}  + \int {\dfrac{1}{{{x^2}}}dx}$ $= \dfrac{{{x^3}}}{3} - 2x - \dfrac{1}{x} + C$.

IV. Tìm hàm số cho biết đạo hàm và giá trị của hàm số tại một điểm

Ví dụ: Tìm hàm số $F\left( x \right)$ biết $F'\left( x \right) = \dfrac{{x - 1}}{{\sqrt[3]{x}}}$ trên $\left( {0; + \infty } \right)$ và $F\left( 1 \right) = 3$.

Giải:

Ta có:

$\begin{array}{l}F'\left( x \right) = \dfrac{{x - 1}}{{\sqrt[3]{x}}} = \left( {x - 1} \right){x^{ - \frac{1}{3}}} = {x^{\frac{2}{3}}} - {x^{ - \frac{1}{3}}}\\ \Rightarrow F\left( x \right) = \int {F'\left( x \right)dx}  = \int {\left( {{x^{\frac{2}{3}}} - {x^{ - \frac{1}{3}}}} \right)dx} \end{array}$

$= \dfrac{{{x^{\frac{2}{3} + 1}}}}{{\dfrac{2}{3} + 1}} - \dfrac{{{x^{ - \frac{1}{3} + 1}}}}{{ - \dfrac{1}{3} + 1}} + C = \dfrac{3}{5}{x^{\frac{5}{3}}} - \dfrac{3}{2}{x^{\frac{2}{3}}} + C$

Lại có $F\left( 1 \right) = 3$ nên $\dfrac{3}{5}{.1^{\frac{5}{3}}} - \dfrac{3}{2}{.1^{\frac{2}{3}}} + C = 3 \Leftrightarrow C = \dfrac{{39}}{{10}}$.

Vậy $F\left( x \right) = \dfrac{3}{5}{x^{\frac{5}{3}}} - \dfrac{3}{2}{x^{\frac{2}{3}}} + \dfrac{{39}}{{10}}$.