I. Các loại chuyển động

II. Chuyển động rơi tự do
I - SỰ RƠI TRONG KHÔNG KHÍ
1. Sự rơi của các vật trong không khí.
Các vật rơi trong không khí xảy ra nhanh chậm khác nhau là do lực cản của không khí tác dụng vào chúng khác nhau.
2. Sự rơi của các vật trong chân không (sự rơi tự do).
- Nếu loại bỏ được ảnh hưởng của không khí thì mọi vật sẽ rơi nhanh như nhau. Sự rơi của các vật trong trường hợp này gọi là sự rơi tự do.
Sự rơi tự do (chuyển động rơi tự do) là sự rơi của các vật chỉ chịu tác dụng của trọng lực.
II - TÍNH CHẤT CỦA CHUYỂN ĐỘNG RƠI TỰ DO
1. Phương, chiều:
- Phương của chuyển động rơi tự do là phương thẳng đứng (phương của dây dọi).
- Chiều của chuyển động rơi tự do là chiều từ trên xuống dưới.
- Tính chất chuyển động: Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều.
2. Công thức của chuyển động rơi tự do
\(\left\{ \begin{array}{l}s = {v_0}t + \frac{1}{2}g{t^2}\\v = {v_0} + gt\\{v^2} - v_0^2 = 2g{\rm{s}}\end{array} \right.\)
Trong đó:
+ \(s\): quãng đường vật rơi được (m)
+ \(v\): vận tốc của vật tại thời điểm t
+ \(g\): gia tốc rơi tự do
Vật được thả rơi \({v_0} = 0\)
3. Gia tốc rơi tự do.
+ Tại một nơi nhất định trên Trái Đất và ở gần mặt đất, các vật đều rơi tự do với cùng một gia tốc g.
+ Ở những nơi khác nhau, gia tốc rơi tự do sẽ khác nhau :
- Ở địa cực g lớn nhất : \(g = 9,8324m/{s^2}\)
- Ở xích đạo g nhỏ nhất : \(g = 9,7872m/{s^2}\)
+ Nếu không đòi hỏi độ chính xác cao, ta có thể lấy \(g = 9,8m/{s^2}\) hoặc \(g = 10m/{s^2}\)
III. Tính tương đối của chuyển động - Công thức cộng vận tốc
I - TÍNH TƯƠNG ĐỐI CỦA CHUYỂN ĐỘNG
1. Tính tương đối của quỹ đạo
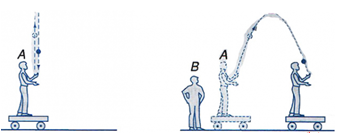
Quỹ đạo của chuyển động có tính tương đối, quỹ đạo trong các hệ quy chiếu khác nhau là khác nhau.
2. Tính tương đối của vận tốc.
Vận tốc của chuyển động có tính tương đối, vận tốc trong các hệ quy chiếu khác nhau là khác nhau.
II - CÔNG THỨC CỘNG VẬN TỐC
1. Hệ qui chiếu đứng yên và hệ qui chiếu chuyển động
- Hệ qui chiếu gắn với vật đứng yên gọi là hệ qui chiếu đứng yên.
- Hệ qui chiếu gắn với vật vật chuyển động gọi là hệ qui chiếu chuyển động.
2. Công thức cộng vận tốc.
\(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
Trong đó:
+ Số 1: gắn với vật cần tính vận tốc
+ Số 2: gắn với hệ quy chiếu là các vật chuyển động
+ Số 3: gắn với hệ quy chiếu là các vật đứng yên
+ \({v_{12}}\): vận tốc của vật so với hệ quy chiếu chuyển động gọi là vận tốc tương đối
+ \({v_{23}}\): vận tốc của hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên gọi là vận tốc kéo theo
+ \({v_{13}}\): vận tốc của vật so với hệ quy chiếu đứng yên gọi là vận tốc tuyệt đối.
- Độ lớn của vận tốc tuyệt đối:
\({v_{13}} = \sqrt {v_{12}^2 + v_{23}^2 + 2{v_{12}}{v_{23}}{\rm{cos}}\alpha } \) với \(\alpha = \left( {\overrightarrow {{v_{12}}} ,\overrightarrow {{v_{23}}} } \right)\)
- Các trường hợp đặc biệt:
- \(\overrightarrow {{v_{12}}} \uparrow \uparrow \overrightarrow {{v_{23}}} \to {v_{13}} = v{}_{12} + {v_{23}}\)
- \(\overrightarrow {{v_{12}}} \uparrow \downarrow \overrightarrow {{v_{23}}} \to {v_{13}} = \left| {v{}_{12} - {v_{23}}} \right|\)
- \(\overrightarrow {{v_{12}}} \bot \overrightarrow {{v_{23}}} \to {v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} \)

