I. Chuyển động ném ngang
1. Khái niệm chuyển động ném ngang
Chuyển động ném ngang là chuyển động có vận tốc ban đầu theo phương nằm ngang và chuyển động dưới tác dụng của trọng lực.
2. Thí nghiệm mô tả chuyển động ném ngang
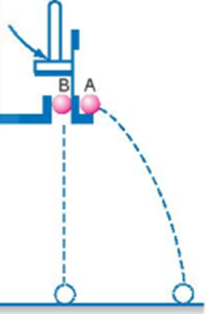
Phân tích chuyển động của 2 vật A và B:
- Vật B rơi tự do
- Vật A chuyển động theo phương ngang với vận tốc v0
Ta có hình ảnh quá trình chuyển động của vật A và B như sau:
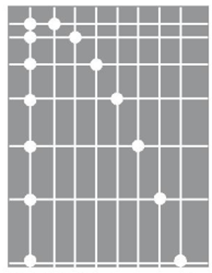
Ta thấy rằng, cả hai vật A và B cùng chạm đất đồng thời
Chuyển động theo phương thẳng đứng của vật A giống với chuyển động rơi tự do của vật B
Điều đó chứng tỏ rằng, vận tốc theo phương ngang của vật A không ảnh hưởng đến chuyển động thẳng đứng của nó. Thời gian rơi tự do cũng bằng thời gian chuyển động theo phương ngang.
Xét chuyển động ném ngang của vật được mô tả như hình vẽ sau:
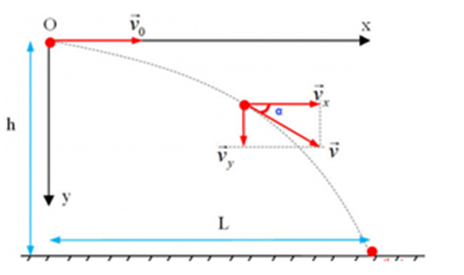
Xét thành phần chuyển động theo phương thằng đứng:
Trên trục Oy:
- Nếu bỏ qua sức cản của không khí thì chuyển động theo phương thẳng đứng của vật là chuyển động rơi tự do với vận tốc ban đầu bằng 0.
- Gia tốc \({a_y} = g\)
- Vận tốc: \({v_y} = gt\)
- Chọn chiều dương từ trên xuống, gọi h là độ cao của vật tại vị trí ném, ta có phương trình chuyển động:
\(y = h = \dfrac{1}{2}g{t^2}\)
- Phương trình quỹ đạo của vật có dạng: \(y = \dfrac{g}{{2{v_0}^2}}.{x^2}\)
Quỹ đạo là một nhánh của đường parabol
- Thời gian rơi của vật: \(t = \sqrt {\dfrac{{2h}}{g}} \)
Xét thành phần chuyển động theo phương ngang:
Trên trục Ox:
- Gia tốc \({a_{\rm{x}}} = 0\), vật chuyển động thẳng đều trên Ox
- Vận tốc: \({v_x} = {v_0}\) là hằng số
- Phương trình chuyển động: \(x = {v_0}t\)
- Tầm xa: Khoảng cách xa nhất ( theo phương ngang ) so với vị trí ném được xác định như sau:
\(L = {x_{max}} = {v_0}.t = {v_0}.\sqrt {\dfrac{{2h}}{g}} \)với t là thời gian rơi của vật
Nhận xét:
+ Tầm xa của vật ném ngang phụ thuộc vào độ cao H của vật khi bị ném và vận tốc ném
+ Cùng một độ cao, ném vật với vận tốc khác nhau, vật có vận tốc ném lớn hơn sẽ có tầm xa lớn hơn
+ Từ các độ cao khác nhau, ném ngang vật với cùng vận tốc thì vật ném ở độ cao lớn hơn thì tầm xa lớn hơn.
II. Chuyển động ném xiên
- Khi ném một quả bóng nên cao theo phương xiên góc với phương nằm ngang, ta thấy quả bóng bay lên rồi rơi xuống theo quỹ đạo có hình dạng parobol như hình ảnh sau:
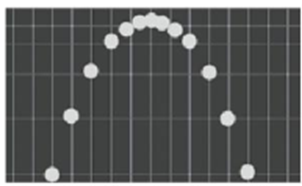
- Chuyển động trên được gọi là chuyển động ném xiên
Chuyển động ném xiên là chuyển động của vật được ném nên với vận tốc ban đầu \(\overrightarrow {{v_0}} \) hợp với phương ngang một góc \(\alpha \)( góc ném ). Vật ném xiên chỉ chịu tác dụng của trọng lực.
Một số hình ảnh ví dụ về chuyển động ném xiên:
1. Phân tích chuyển động ném xiên
Ta phân tích chuyển động của vật ném xiên thành hai chuyển động thành phần: chuyển động theo phương thẳng đứng và chuyển động theo phương nằm ngang.
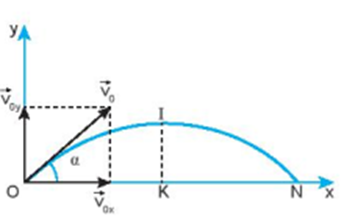Theo phương ngang : vật không chịu tác dụng của lực nào, nên vật chuyển động thẳng đều.
Theo phương thẳng đứng:
+ Giai đoạn 1: Vật chuyển động đi lên đến độ cao cực đại \(\left( {{v_y} = 0} \right)\), sau đó chịu tác dụng của trọng lực nên vật chậm dần đều với gia tốc -g
+ Giai đoạn 2: Vật chuyển động đi xuống tương đương như chuyển động ném ngang.
Độ lớn lực không đổi, nên có thời gian vật chuyển động đi lên đến độ cao cực đại bằng với thời gian vật chuyển động đi xuống ngang với vị trí ném.
2. Các công thức trong chuyển động ném xiên
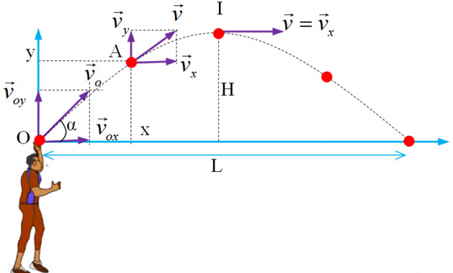
- Phương trình vận tốc của chuyển động ném xiên:
Theo phương Ox: \({v_x} = {v_0}{\rm{.cos}}\alpha \)
Theo phương Oy (vật đi lên) : \({v_y} = {v_0}.\sin \alpha - gt\)
Theo phương Oy ( vật đi xuống): \({v_y} = gt\)
Liên hệ giữa vx và vy: \(\tan \alpha = \dfrac{{{v_y}}}{{{v_x}}}\)
Độ lớn của vậnt tốc tại vị trí bất kì: \(v = \sqrt {v_x^2 + v_y^2} \)
- Phương trình chuyển động, tọa độ của chuyển động ném xiên:
\(x = {v_x}t = ({v_0}.co{\rm{s}}\alpha {\rm{)}}{\rm{.t}}\)
Đi lên: \(y = {v_0}\sin \alpha .t - \dfrac{1}{2}g{t^2}\)
Đi xuống: \(y = \dfrac{1}{2}g{t^2}\)
Quỹ đạo đi lên:
\(y = \left( {\dfrac{{ - g}}{{2v_0^2co{{\rm{s}}^2}\alpha }}} \right){x^2} + x\tan \alpha \)
Quỹ đạo đi xuống:
\(y = \left( {\dfrac{g}{{2v_0^2co{{\rm{s}}^2}\alpha }}} \right){x^2}\)
Chuyển động ném xiên có quỹ đạo là đường parabol
- Các công thức khác:
Thời gian vật đạt độ cao cực đại:
\({t_1} = \dfrac{{{v_0}\sin \alpha }}{g}\)
Tầm cao ( độ cao cực đại của vật ):
\(H = \dfrac{{v_0^2{{\sin }^2}\alpha }}{{2g}}\)
Thời gian vật đi từ H đến khi rơi xuống đất:
\({t_2} = \sqrt {\dfrac{{2(H + h)}}{g}} \)
Thời gian chạm đất kể từ lúc ném: \(t = {t_1} + {t_2}\)
Tầm xa: \(L = {v_0}cos\alpha ({t_1} + {t_2}) = \dfrac{{v_0^2\sin 2\alpha }}{{2g}} + {v_0}co{\rm{s}}\alpha \sqrt {\dfrac{{2(H + h)}}{g}} \)
Trong đó: h là độ cao của vật so với vị trí ném, nếu ném tại mặt đất thì h=0
