I. Lý thuyết chuyển động tròn đều
1. Chuyển động tròn đều
Chuyển động tròn: là chuyển động có quỹ đạo là một đường tròn
Tốc độ trung bình trong chuyển động tròn: bằng thương số giữa độ dài cung tròn \(\Delta s\) mà vật đi được và thời gian \(\Delta t\)đi hết cung tròn đó \({\upsilon _{tb}} = \dfrac{{\Delta s}}{{\Delta t}}\)
Chuyển động tròn đều: là chuyển động có quỹ đạo tròn và có tốc độ trung bình trên mọi cung tròn là như nhau.
2. Vecto vận tốc trong chuyển động tròn đều
- Tốc độ dài: Trong chuyển động tròn đều, tốc đọ dài của vật có độ lớn không đổi
\(\upsilon = \dfrac{{\Delta s}}{{\Delta t}} = con{\rm{s}}t\)
\(\Delta s\) là độ dài cung tròn (coi như thẳng) mà vật đi được trong khoảng thời gian rất nhỏ \(\Delta t\)
- Vecto vận tốc: \(\vec v = \dfrac{{\Delta \vec s}}{{\Delta t}}\)
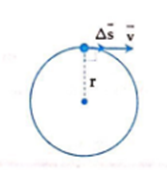
+ Gốc trên vật chuyển động
+ Phương tiếp tuyến với đường tròn tại vị trí của vật
+ Chiều: trùng với chiều chuyển động của vật
3. Tốc độ góc – chu kì – Tần số
- Tốc độ góc: là đại lượng đo bằng góc mà bán kính quay quét được trong một đơn vị thời gian, là đại lượng không đổi.
\(\omega = \dfrac{{\Delta s}}{{\Delta t}} = con{\rm{s}}t\)(đơn vị: rad/s)
- Chu kì: là thời gian để vật quay hết 1 vòng.
\(T = \dfrac{{2\pi }}{\omega }\) (đơn vị:s)
- Tần số: là số vòng mà vật đi được trong 1 giây
\(f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}\) (đơn vị: vòng/s hay Hz)
chú ý: mối quan hệ giữa \(\upsilon \) và \(\omega \): \(\upsilon = \omega r\)
4. Gia tốc hướng tâm
Gia tốc trong chuyển động tròn đều luôn hướng vào tâm quỹ đạo, gọi là gia tốc hướng tâm \(\overrightarrow {{a_{ht}}} \) có:
- Gốc: trên vật chuyển động
- Phương: là phương bán kính.
- Chiều: hướng vào tâm đường tròn quỹ đạo
- Độ lớn: \({a_{ht}} = \dfrac{{{v^2}}}{R} = {\omega ^2}R\)
với R là bán kính đường tròn
- Gia tốc hướng tâm chỉ có tác dụng làm thay đổi hướng vận tốc chứ không làm thay đổi độ lớn của vận tốc
II. Các dạng bài tập chuyển động tròn
1. Dạng 1: Tìm các đại lượng
- Công thức tính chu kỳ: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{L}{n} = \dfrac{{2\pi R}}{v}\)
- Công thức tần số: \(f = \dfrac{1}{T} = \dfrac{\omega }{{2\pi }}\)
- Công thức liên hệ giữa tốc độ dài và tốc độ góc: \(v = R\omega \)
2. Dạng 2: Các bài toán liên quan đến gia tốc hướng tâm
- Áp dụng công thức gia tốc hướng tâm: \({a_{ht}} = \dfrac{{{v^2}}}{R} = R.{\omega ^2}\)
3. Những lưu ý khi giải bài tập chuyển động tròn đều
- Cần phân biệt tốc độ dài và vận tốc dài, tốc độ dài và tốc độ góc, đường đi ( cung tròn ) và góc quay \(\varphi \).
- Các đặc điểm của chuyển động tròn đều:
+ Tốc độ dài và tốc độ góc luôn không đổi: \(v = con{\rm{s}}t;\omega = con{\rm{s}}t\)
+ Gia tốc là gia tốc hướng tâm: \({a_{ht}} = \dfrac{{{v^2}}}{R} = R{\omega ^2}\)
- Các phương trình tọa độ của chuyển động tròn có thể được viết dưới dạng:
theo tọa độ cong: \(s = {s_0} + vt\)
theo tọa độ góc: \(\alpha = {\alpha _0} + \omega t\)
- Nếu trong khoảng thời gian \(\Delta t\) vật quay được n vòng thì \(\Delta t = nT\)
- Liên hệ giữa tọa độ cong và tọa độ góc: \(s = R.\varphi \)
- Hai kim giờ - phút lúc \(t = 0\) lệch nhau góc \(\alpha \)
\( \Rightarrow \)thời điểm lệch nhau góc \(\alpha \) lần thứ n được xác định bởi: \({t_n} = {\omega _{ph}} - {\omega _g} = \alpha + 2n\pi \)
- Vận tốc dài và gia tốc hướng tâm của một điểm trên mặt đất phụ thuộc vào vĩ độ \(\varphi \)
- Khi vật vừa quay tròn đều, vừa tịnh tiến thì:
+ Khi vật có hình tròn lăn không trượt, độ dài cung quay của một điểm trên vành bằng quãng đường đi được
+ Vận tốc của một điểm đối với mặt đất được xác định bằng công thức cộng vận tốc
