I. Chuyển động thẳng đều
I- CHUYỂN ĐỘNG THẲNG ĐỀU
1. Định nghĩa
Chuyển động thẳng đều là chuyển động thẳng, trong đó chất điểm có vận tốc tức thời không đổi.
Định nghĩa khác: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.
- Đặc điểm của chuyển động thẳng đều
+ Quỹ đạo chuyển động: là một đường thẳng
+ Vận tốc chuyển động: không đổi
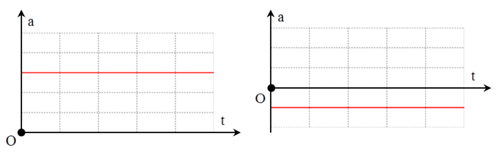
+ Gia tốc chuyển động: bằng không
- Công thức liên hệ giữa v - s - t của chuyển động thẳng đều
\(v = \dfrac{s}{t}\)
Trong đó:
+ v: vận tốc của chuyển động thẳng đều
+ s: quãng đường đi được
+ t: thời gian đi hết quãng đường s
2. Phương trình chuyển động thẳng đều
\(x = {x_0} + v(t - {t_0})\)
Trong đó:
+ x: tọa độ của vật tại thời điểm t
+ x0: tọa độ của vật tại thời điểm ban đầu t0
+ v: vận tốc tức thời (gọi tắt là vận tốc) của vật
+ t0: gốc thời gian
+ Để đơn giản: ta chọn gốc thời gian t0 = 0
+ Quãng đường vật đi được sau khoảng thời gian \(\Delta t\) : \(s = \left| v \right|\Delta t\)
+ Nếu vật chuyển động thẳng và không đổi chiều ta có: \(\Delta x = x - {x_0} = s\)(độ dời bằng quãng đường)
+ Dấu của vận tốc phụ thuộc vào chiều dương mà ta chọn, nếu vật chuyển động cùng chiều dương \(v > 0\) , vật chuyển động ngược chiều dương \(v < 0\).
II- ĐỒ THỊ CỦA CHUYỂN ĐỘNG THẲNG ĐỀU
1. Đồ thị tọa độ theo thời gian (x - t)
\(x = {x_0} + vt\) dạng đồ thị giống đồ thị của hàm số \(y = ax + b\)
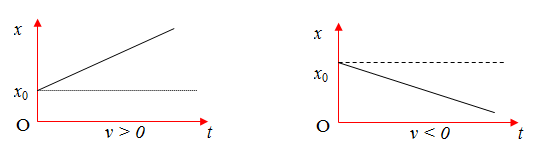
Độ dốc của đường thẳng:
\(tag\alpha = \dfrac{{x - {x_0}}}{t} = v\)
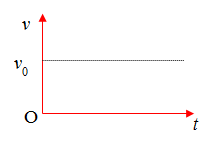
2. Đồ thị vận tốc theo thời gian (v - t)
Trong chuyển động thẳng đều, vận tốc không thay đổi \(v = {v_0}\)
Đồ thị biểu diễn vận tốc theo thời gian là một đường thẳng song song với trục thời gian.
III- CÁC DẠNG BÀI TẬP
1. Tính vận tốc, tốc độ trung bình
Vận dụng công thức: \(v = \dfrac{s}{t}\)
\(v = \dfrac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}}\)
2. Lập phương trình chuyển động - Xác định vị trí và thời điểm hai vật gặp nhau
- Lập phương trình chuyển động
+ Bước 1: Chọn hệ quy chiếu (HQC)
- Trục tọa độ: Ox trùng với quỹ đạo chuyển động
- Gốc tọa độ (thường gắn với vị trí ban đầu của vật)
- Gốc thời gian: (lúc vật bắt đầu chuyển động
- Chiều dương: thường chọn chiều chuyển động của vật làm gốc
+ Bước 2: Xác định gốc tọa độ và gốc thời gian
+ Bước 3: Xác định vận tốc
+ Bước 4: Viết phương trình chuyển động
- Xác định vị trí và thời điểm hai vật gặp nhau
+ Khi hai vật gặp nhau thì \({x_1} = {x_2}\)
+ Khi hai vật cách nhau một khoảng \(\Delta s\) thì \(\left| {{x_1} - {x_2}} \right| = \Delta s\)
II. Chuyển động thẳng biến đổi đều
I - CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU
1. Định nghĩa
Chuyển động thẳng biến đổi là chuyển động thẳng trong đó gia tốc tức thời không đổi

2. Các phương trình của chuyển động thẳng biến đổi đều
- Gia tốc:
\(\overrightarrow a = \dfrac{{\overrightarrow v - \overrightarrow {{v_0}} }}{{\Delta t}}\) có độ lớn: \(a = \dfrac{{v - {v_0}}}{{\Delta t}}\)
- Phương trình tọa độ - thời gian của chuyển động thẳng biến đổi đều
\(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\)
Trong đó:
+ x0 : tọa độ ban đầu của chất điểm
+ v0: Vận tốc của chất điểm tại thời điểm ban đầu (tại t = 0)
+ t: thời gian chuyển động
- Phương trình vận tốc:
\(v = {v_0} + at\)
Trong đó:
+ v0: Vận tốc của chất điểm tại thời điểm ban đầu (tại t = 0)
+ a: gia tốc
+ t: thời gian chuyển động
- Hệ thức độc lập thời gian:
\({v^2} - v_0^2 = 2{\rm{a}}\Delta {\rm{x}}\)
\((\Delta x = x - {x_0})\) là độ dời trong khoảng thời gian từ 0 đến t
II- ĐỒ THỊ CỦA CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU
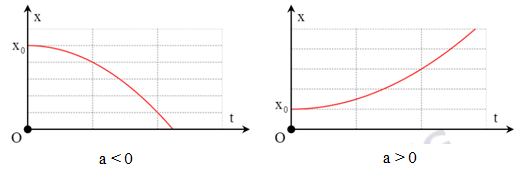
1. Đồ thị tọa độ theo thời gian (x - t)
Là nhánh parabol
2. Đồ thị vận tốc theo thời gian (v - t)
Là đường thẳng xiên góc.
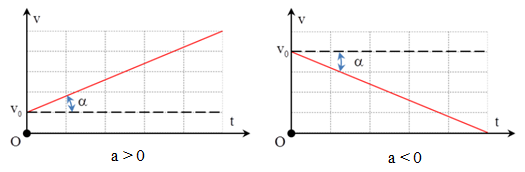
Hệ số góc của đường biểu diễn v - t bằng gia tốc của chuyển động: \(a = \tan \alpha = \frac{{v - {v_0}}}{t}\)
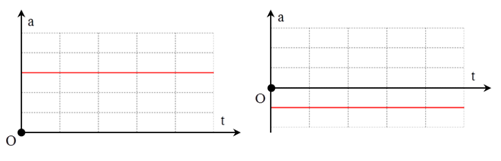
3. Đồ thị gia tốc theo thời gian (a - t)
Là đường thẳng song song với trục Ot
III. Các dạng bài tập chuyển động thẳng biến đổi đều
I- DẠNG 1: XÁC ĐỊNH CÁC ĐẠI LƯỢNG: QUÃNG ĐƯỜNG - VẬN TỐC - GIA TỐC
Phương pháp:
+ Chọn hệ quy chiếu
+ Áp dụng các công thức: \(\left\{ \begin{array}{l}x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\\v = {v_0} + at\end{array} \right.\)
- Vận tốc nhận giá trị dương nếu vật chuyển động cùng chiều dương, nhận giá trị âm nếu vật chuyển động ngược chiều dương.
- Vật chuyển động nhanh dần đều thì a.v > 0, vật chuyển động chậm dần đều thì a.v < 0
- Trong hệ đơn vị SI thì: s(m); v(m/s); a(m/s2) và \(1km/h = \frac{1}{{3,6}}m/s\)
II- DẠNG 2: VIẾT PHƯƠNG TRÌNH CHUYỂN ĐỘNG
Phương pháp:
- Bước 1: Chọn hệ quy chiếu
+ Chọn trục tọa độ Ox
+ Chọn mốc thời gian t = 0
- Bước 2: Viết phương trình chuyển động
\(x = {x_0} + {v_0}t + \frac{1}{2}a{t^2}\)
+ \({x_0}\): là tọa độ ban đầu của chất điểm (\({x_0}\)lấy giá trị dương nếu chất điểm nằm ở phía dương của trục tọa độ ấy, lấy giá trị âm nếu chất điểm nằm ở phía âm của trục tọa độ ấy)
+ v0: vận tốc của vật tại thời điểm ban đầu (t = 0) (v0 lấy giá trị dương nếu chất điểm chuyển động cùng chiều dương và lấy giá trị âm nếu chất điểm chuyển động ngược chiều dương)
+ Vật chuyển động nhanh dần đều thì av > 0, chuyển động chậm dần đều thì av < 0.
+ t: thời gian chuyển động
III- DẠNG 3: ĐỒ THỊ CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU
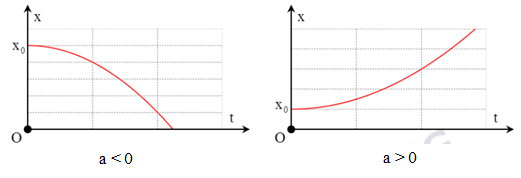
1. Đồ thị tọa độ theo thời gian (x - t)
Là nhánh parabol
2. Đồ thị vận tốc theo thời gian (v - t)
Là đường thẳng xiên góc.
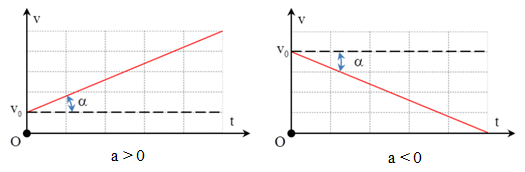
Hệ số góc của đường biểu diễn v - t bằng gia tốc của chuyển động: \(a = \tan \alpha = \frac{{v - {v_0}}}{t}\)
3. Đồ thị gia tốc theo thời gian (a - t)
Là đường thẳng song song với trục Ot