Độ dịch chuyển và quãng đường đi được

I. Vị trí của vật chuyển động tại các thời điểm

- Cách xác định vị trí của vật: dùng hệ tọa độ vuông góc có gốc là vị trí của vật mốc, trục hoành Ox và trục tung Oy. Các giá trị trên các trục tọa độ được xác định theo một tỉ lệ xác định.

Ví dụ: Nếu tỉ lệ là \(\dfrac{1}{{1000}}\) thì vị trí của điểm A trong Hình 4.1 được xác định trên hệ tọa độ là A (x = 10 m; y = 20 m) và của điểm B là B (x = -10 m; y = 20 m).

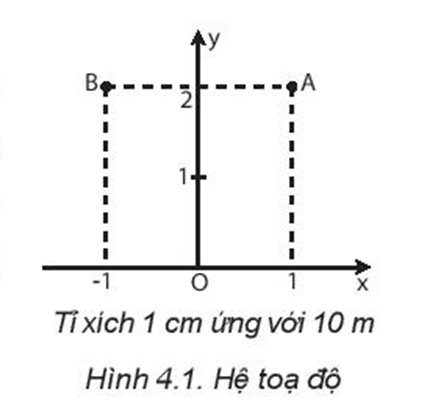
- Cách xác định thời điểm: Chọn mốc thời gian, đo khoảng cách thời gian từ thời điểm được chọn làm mốc đến thời điểm cần xác định.

Ví dụ: Nếu chọn mốc thời gian là lúc 6 h và thời gian chuyển động là 2 h thì thời điểm kết thúc là 2 + 6 = 8 h.

II. Độ dịch chuyển

- Độ dịch chuyển ( hay còn được gọi là độ dời) được biểu diễn bằng một mũi tên nối vị trí đầu và vị trí cuối của chuyển động, có độ dài tỉ lệ với độ lớn của độ dịch chuyển.

- Kí hiệu: \(\overline d \)

- Đơn vị: m.

Ví dụ: Một vật di chuyển từ A đến B được 500 m, rồi quay về C là 150 m. Hỏi độ dịch chuyển của vật này là bao nhiêu?

Cách giải:

Ta có: điểm đầu tại A, điểm kết thúc tại C, nên độ dịch chuyển \(\overline d  = AC = 500 - 150 = 350(m)\)

III. Phân biệt độ dịch chuyển và quãng đường đi được

- Độ dịch chuyển là khoảng cách từ vị trí đầu đến vị cuối của vật, cho biết độ dài và sự thay đổi vị trí của vật

- Quãng đường là độ dài của vật thực hiện được trong suốt quá trình chuyển động.

Ví dụ: Một vật di chuyển từ A đến B được 500 m, rồi quay về C là 150 m. Hỏi độ dịch chuyển và quãng đường của vật này là bao nhiêu?

Cách giải:

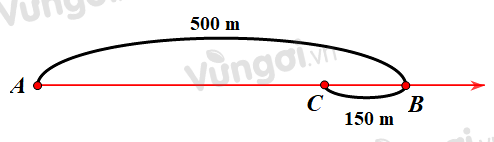
Độ dịch chuyển: \(\overline d  = AC = 500 - 150 = 350(m)\)

Quãng đường: s = AB + BC = 500 + 150 = 650 (m).

IV. Tổng hợp độ dịch chuyển

- Dùng phép cộng vectơ để tổng hợp độ dịch chuyển của vật.

- Phép cộng vectơ: \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)