Câu hỏi:
3 năm trước
Cho tam giác $ABC$ cân tại $A$ . Trên cạnh $AC$ lấy điểm $M$ , trên đoạn thẳng $BM$ lấy điểm $K$ sao cho $\widehat {BCK} = \widehat {ABM}$ .
Tam giác \(MBC\) đồng dạng với tam giác
Trả lời bởi giáo viên
Đáp án đúng: a
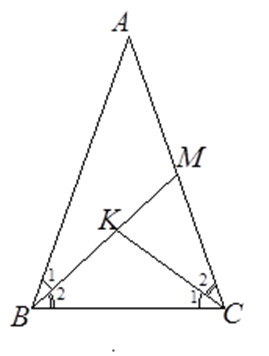
Tam giác $ABC$ cân tại $A$ nên $\widehat {ABC} = \widehat {ACB}$, ta lại có $\widehat {{B_1}} = \widehat {{C_1}}$ (gt) nên $\widehat {{B_2}} = \widehat {{C_2}}$ .
$\Delta MBC$ và $\Delta MCK$có
$\widehat {BMC}$ là góc chung;
$\widehat {{B_2}} = \widehat {{C_2}}$ (chứng minh trên).
Do đó $\Delta MBC\backsim\Delta MCK$ (g.g).
Hướng dẫn giải:
- Chứng minh 2 tam giác đồng dạng theo trường hợp góc – góc.
Giải thích thêm:
- Học sinh cần viết các cặp tam giác đồng dạng theo đúng thứ tự đỉnh tương ứng của 2 tam giác.