Bài tập định luật Ôm cho đoạn mạch có các điện trở mắc nối tiếp

Ta có điện trở tương đương của đoạn mạch \({R_{12}} = 40\Omega \) (tính ở câu trên)

+ Cường độ dòng điện của đoạn mạch là: \(I = \frac{U}{{{R_{12}}}} = \frac{{16}}{{40}} = 0,4{\rm{A}}\)

+ Hiệu điện thế giữa hai đầu của mỗi điện trở là: \(\left\{ \begin{array}{l}{U_1} = I{R_1} = 0,4.24 = 9,6{\rm{ }}V\\{U_2} = I{R_2} = 0,4.16 = 6,4V\end{array} \right.\)  

Ta có điện trở tương đương\({R_{12}}\) của đoạn mạch:

\({R_{12}} = {R_1} + {R_2} = 24 + 16 = 40\Omega \)

Ta có điện trở tương đương\({R_{12}}\) của đoạn mạch:

\({R_{12}} = {R_1} + {R_2} = 24 + 16 = 40\Omega \)

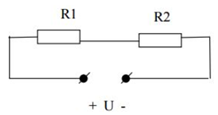
Cường độ dòng điện chạy trong mạch: \(I = {I_1} = {I_2} = \dfrac{U}{{{R_{td}}}} = \dfrac{U}{{{R_1} + {R_2}}} = \dfrac{{18}}{{4 + 2}} = 3A\)

→ Hiệu điện thế hai đầu điện trở R₂ là:

\({U_2} = {I_2}.{R_2} = 3.2 = 6V\)

Ta có: \(\left\{ \begin{array}{l}R = {R_1} + {R_2}\\{R_1} > {R_2}\end{array} \right. \Rightarrow R > {R_1}\)

Công thức của đoạn mạch các điện trở mắc nối tiếp: \(\left\{ \begin{array}{l}{R_{td}} = {R_1} + {R_2}\\I = {I_1} = {I_2}\\U = {U_1} + {U_2}\end{array} \right.\)

→ Phát biểu đúng: Trong đoạn mạch mắc nối tiếp, cường độ dòng điện có giá trị như nhau tại mọi điểm

Ta có : \(\left\{ \begin{array}{l}U = {U_1} + {U_2} + {U_3}\\I = {I_1} = {I_2} = {I_3}\\{R_{td}} = {R_1} + {R_2} + {R_3}\end{array} \right.\)

Có : \({I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{6}{3} = 2A \Rightarrow I = {I_1} = {I_3} = 2A\)

Có : \(\left\{ \begin{array}{l}{I_3} = 2A\\{R_3} = 4\Omega \end{array} \right. \Rightarrow {U_3} = {I_3}{R_3} = 8V \Rightarrow U = {U_1} + {U_2} + {U_3} = 6 + 8 + 8 = 22V\)

Đoạn mạch gồm hai điện trở mắc nối tiếp: \(I = {I_1} = {I_2}\)

Để mạch điện không bị hỏng thì: \(\left\{ \begin{array}{l}I \le {I_{1\max }}\\I \le {I_{2\max }}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}I \le 4A\\I \le 3A\end{array} \right. \Rightarrow I \le 3A\)

→ Cường độ dòng điện lớn nhất chạy qua mạch là: I_max = 3A

→ Hiệu điện thế tối đa được phép đặt vào hai đầu đoạn mạch này là:

\({U_{\max }} = {I_{\max }}.{R_{td}} = {I_{\max }}.\left( {{R_1} + {R_2}} \right) = 3.\left( {15 + 30} \right) = 135V\)

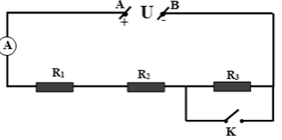
- Khi K mở: Mạch gồm (R₁ nt R₂ nt R₃):

→ Điện trở tương đương của đoạn mạch là: R_tđm = R₁ + R₂ + R₃ = 4 + 5 + R₃ = 9 + R₃

Cường độ dòng điện qua 3 điện trở là như nhau nên số chỉ của ampe lúc này là:

 \({I_m} = \dfrac{U}{{{R_{tdm}}}} = \dfrac{U}{{9 + {R_3}}}\,\,\,\,\,\left( 1 \right)\)

- Khi K đóng, điện trở R₃ bị nối tắt nên mạch chỉ còn hai điện trở R₁, R₂ ghép nối tiếp.

→ Điện trở tương đương của đoạn mạch khi K đóng là: R_tđđ = R₁ + R₂ = 4 + 5 = 9 Ω

Số chỉ của ampe lúc này là: \({I_d} = \dfrac{U}{{{R_{tdd}}}} = \frac{U}{9}\,\,\,\,\,\left( 2 \right)\)

- Từ (1) và (2) ta thấy I_đ  >  I_m, nên theo đề bài ta có: I_đ = 3I_m (3)

Từ (1), (2) và (3) ta có: \(\dfrac{U}{9} = 3.\dfrac{U}{{9 + {R_3}}} \Rightarrow {R_3} = 18\Omega \)

Ta có: \(\left\{ \begin{array}{l}\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{I.{R_1}}}{{I.{R_2}}}\\{R_2} = 1,5.{R_1}\end{array} \right. \Rightarrow \dfrac{{{U_1}}}{{{U_2}}} = \dfrac{1}{{1,5}} \Rightarrow {U_2} = 1,5{U_1} = 4,5V \Rightarrow U = {U_1} + {U_2} = 3 + 4,5 = 7,5V\)

Điện trở tương đương của đoạn mạch là: \({R_{td}} = {R_1} + {R_2} + {R_3} = 5 + 10 + 15 = 30\Omega \)

Ta có :

\(\begin{array}{l}\left\{ \begin{array}{l}{U_{AC}} = {U_1} = {I_1}{R_1}\\{U_{CB}} = {U_2} = {I_2}{R_2}\end{array} \right.\\I = \dfrac{{{U_{AB}}}}{{{R_{td}}}} = \dfrac{{84}}{{600}} = 0,14A = {I_1} = {I_2}\\{R_{td}} = {R_1} + {R_2} = 400 + 200 = 600\Omega \\ \Rightarrow \left\{ \begin{array}{l}{U_{AC}} = {U_1} = {I_1}{R_1} = 0,14.400 = 56V\\{U_{CB}} = {U_2} = {I_2}{R_2} = 0,14.200 = 28V\end{array} \right.\end{array}\)

Ta có: \(\left\{ \begin{array}{l}{R_{td}} = {R_1} + {R_2} = 20\Omega \\I = {I_1} = {I_2} = 2A\\U = I.{R_{td}} = 2.20 = 40V\\{U_2} = {I_2}{R_2} = 2.15 = 30V\end{array} \right.\)

Ta có điện trở tương đương\({R_{12}}\) của đoạn mạch:

\({R_{12}} = {R_1} + {R_2} = 24 + 16 = 40\Omega \)

Khi hai điện trở mắc nối tiếp thì điện trở tương đương là:

\({R_{td}} = {R_1} + {R_2} = 20 + 60 = 80\Omega \)

Cường độ dòng điện chạy trong mạch là:  

\(I = \frac{U}{{{R_{td}}}} = \frac{8}{{80}} = 0,1A\)

Hiệu điện thế hai đầu R₁ là: 

\({U_1} = I.{R_1} = 0,1.20 = 2V\)

Điện trở tương đương: \({R_{t}} = {R_1} + {R_2} + {R_3} = 5 + 10 + 15 = 30\Omega \)

Ta có, trong đoạn mạch mắc nối tiếp thì:

Cường độ dòng điện có giá trị như nhau tại mọi điểm: \(I = {I_1} = {I_2} =  \ldots  = {I_n}\)          

A, B, D - đúng

C - sai vì: Hiệu điện thế giữa hai đầu đoạn mạch bằng tổng hiệu điện thế giữa hai đầu mỗi điện trở thành phần: \(U = {U_1} + {U_2} +  \ldots  + {U_n}\)

B, C, D - là các đặc điểm của đoạn mạch mắc nối tiếp

A - không phải là đặc điểm của đoạn mạch mắc nối tiếp vì: đoạn mạch có những điểm nối chung của nhiều điện trở thì có thể là mạch rẽ nhánh, phân nhánh => đó không phải là mạch nối tiếp

Ta có: Điện trở tương đương của đoạn mạch nối tiếp bằng tổng các điện trở hợp thành: \({R_{td}} = {R_1} + {R_2}\)