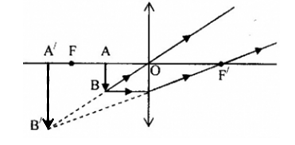
Ảnh của vật \(AB\) là \(A'B'\) có độ lớn bằng:
- Cách 1:
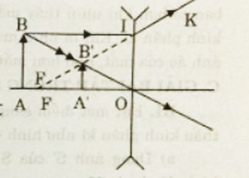
+ Từ hình, ta có:
- \(\Delta FB'O\) đồng dạng với \(\Delta IB'B\)
Ta suy ra: $\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}} = \frac{8}{{12}} = \frac{2}{3}$
- \(\Delta OAB\) đồng dạng với \(\Delta OA'B'\)
Ta suy ra:
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{OB}}{{OB'}} = \frac{{OB' + BB'}}{{OB'}} = 1 + \frac{2}{3} = \frac{5}{3}\\ \to A'B' = \frac{3}{5}AB = \frac{3}{5}.6 = 3,6mm\end{array}\)
- Cách 2: Sử dụng công thức tỉ lệ ảnh vật: \(\frac{h}{{h'}} = \frac{d}{{d'}}\)
Ta có: \(\left\{ \begin{array}{l}h = 6mm\\d = 8cm\\d' = 4,8cm\end{array} \right.\)
\( \to \frac{h}{{h'}} = \frac{d}{{d'}} \to h' = \frac{{d'}}{d}h = \frac{{4,8}}{8}.6 = 3,6mm\)
Ảnh của vật \(AB\) cách thấu kính một đoạn bằng:
- Cách 1:
+ Ta có, ảnh của vật qua thấu kính phân kì
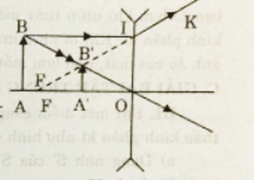
+ Từ hình, ta có:
- \(\Delta FB'O\) đồng dạng với \(\Delta IB'B\)
Ta suy ra: $\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}} = \frac{8}{{12}} = \frac{2}{3}$
- \(\Delta OAB\) đồng dạng với \(\Delta OA'B'\)
Ta suy ra:
\(\begin{array}{l}\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OB' + BB'}}{{OB'}} = 1 + \frac{{BB'}}{{OB'}} = 1 + \frac{2}{3} = \frac{5}{3}\\ \to OA' = \frac{3}{5}OA = \frac{3}{5}8 = 4,8cm\end{array}\)
- Cách 2: Sử dụng công thức thấu kính phân kì: \(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d}\)
Ta có: \(\left\{ \begin{array}{l}f = 12cm\\d = 8cm\\d' = ?\end{array} \right.\)
\(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d} \to d' = \frac{{f{\rm{d}}}}{{f + d}} = \frac{{12.8}}{{12 + 8}} = 4,8cm\)
Ảnh của vật \(AB\) cách thấu kính một đoạn bằng:
- Cách 1:
+ Ta có, ảnh của vật qua thấu kính phân kì
+ Từ hình, ta có:
- \(\Delta FB'O\) đồng dạng với \(\Delta IB'B\)
Ta suy ra: $\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}} = \frac{8}{{12}} = \frac{2}{3}$
- \(\Delta OAB\) đồng dạng với \(\Delta OA'B'\)
Ta suy ra:
\(\begin{array}{l}\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OB' + BB'}}{{OB'}} = 1 + \frac{{BB'}}{{OB'}} = 1 + \frac{2}{3} = \frac{5}{3}\\ \to OA' = \frac{3}{5}OA = \frac{3}{5}8 = 4,8cm\end{array}\)
- Cách 2: Sử dụng công thức thấu kính phân kì: \(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d}\)
Ta có: \(\left\{ \begin{array}{l}f = 12cm\\d = 8cm\\d' = ?\end{array} \right.\)
\(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d} \to d' = \frac{{f{\rm{d}}}}{{f + d}} = \frac{{12.8}}{{12 + 8}} = 4,8cm\)
Ảnh của vật \(AB\) cách thấu kính một đoạn bằng:
- Cách 1:
+ Ta có, ảnh của vật qua thấu kính phân kì
+ Từ hình, ta có:
- \(\Delta FB'O\) đồng dạng với \(\Delta IB'B\)
Ta suy ra: $\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}} = \frac{8}{{12}} = \frac{2}{3}$
- \(\Delta OAB\) đồng dạng với \(\Delta OA'B'\)
Ta suy ra:
\(\begin{array}{l}\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OB' + BB'}}{{OB'}} = 1 + \frac{{BB'}}{{OB'}} = 1 + \frac{2}{3} = \frac{5}{3}\\ \to OA' = \frac{3}{5}OA = \frac{3}{5}8 = 4,8cm\end{array}\)
- Cách 2: Sử dụng công thức thấu kính phân kì: \(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d}\)
Ta có: \(\left\{ \begin{array}{l}f = 12cm\\d = 8cm\\d' = ?\end{array} \right.\)
\(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d} \to d' = \frac{{f{\rm{d}}}}{{f + d}} = \frac{{12.8}}{{12 + 8}} = 4,8cm\)
Ảnh của một ngọn nến qua một thấu kính phân kì:
Ta có ảnh của một vật qua thấu kính phân kì luôn là ảnh ảo, cùng chiều và nhỏ hơn vật.
Đặt một vật sáng AB trước thấu kính phân kỳ thu được ảnh A’B’ là:
Ta có ảnh của một vật qua thấu kính phân kì luôn là ảnh ảo, cùng chiều và nhỏ hơn vật.
Đối với thấu kính phân kỳ, khi vật đặt rất xa thấu kính thì ảnh ảo của vật tạo bởi thấu kính:
Vật đặt rất xa thấu kính, ảnh ảo của vật có vị trí cách thấu kính một khoảng bằng tiêu cự.
Ảnh ảo của một vật tạo bởi thấu kính phân kỳ và thấu kính hội tụ giống nhau ở chỗ
A - đúng
B - sai vì ảnh ảo của vật qua thấu kính hội tụ và thấu kính phân kì đều cùng chiều với vật
C - sai vì ảnh ảo của vật qua thấu kính hội tụ lớn hơn vật còn ảnh ảo của vật qua thấu kính phân kì luôn nhỏ hơn vật.
D - sai vì ảnh ảo của vật qua thấu kính hội tụ lớn hơn vật còn ảnh ảo của vật qua thấu kính phân kì luôn nhỏ hơn vật.
Vật sáng AB được đặt vuông góc với trục chính tại tiêu điểm của một thấu kính phân kỳ có tiêu cự f. Nếu dịch chuyển vật lại gần thấu kính thì ảnh ảo của vật sẽ
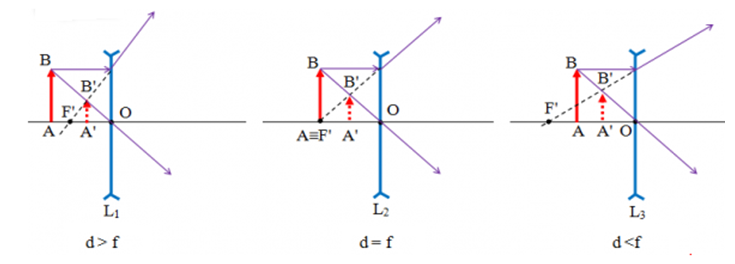
Sử dụng đặc điểm ảnh của một vật tạo bởi thấu kính phân kì
Nếu dịch chuyển vật lại gần thấu kính thì ảnh ảo của vật sẽ càng lớn và càng gần thấu kính.
Vật đặt ở vị trí nào trước thấu kính phân kì cho ảnh trùng vị trí tiêu điểm:
Vật đặt rất xa thấu kính, ảnh ảo của vật có vị trí cách thấu kính một khoảng bằng tiêu cự.
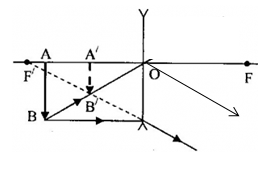
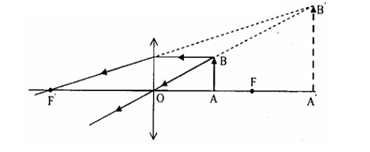
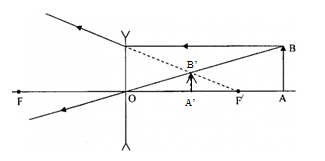
Chọn phương án đúng về cách vẽ ảnh \(A'B'\) của vật sáng \(AB\) trong các trường hợp sau:
A - sai vì: ảnh \(A'B'\) là ảnh ảo
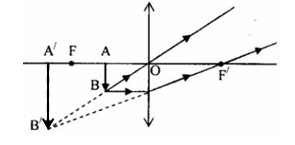
B - sai vì: tia đi qua quang tâm thì truyền thẳng
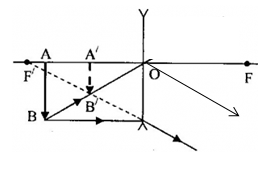
C - đúng
D - sai vì: ảnh \(A'B'\) là ảnh ảo
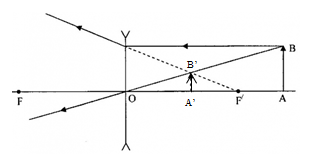
Vật \(AB\) có độ cao \(h\) được đặt vuông góc với trục chính của một thấu kính phân kì. Điểm \(A\) nằm trên trục chính và có vị trí tại tiêu điểm \(F\). Ảnh \(A'B'\) có độ cao là \(h'\) thì:
+ Ta có: \(d' = \frac{f}{2}\)
+ Ta suy ra: \(\frac{h}{{h'}} = \frac{d}{{d'}} = \frac{f}{{\frac{f}{2}}} = 2 \to h = 2h'\)
Lần lượt đặt vật \(AB\) trước thấu kính phân kì và thấu kính hội tụ. Thấu kính phân kì cho ảnh ảo \({A_1}{B_1}\) , thấu kính hội tụ cho ảnh ảo \({A_2}{B_2}\) thì:
Ta có:
+ Vật qua thấu kính hội tụ cho ảnh ảo thì ảnh ảo luôn lớn hơn vật
+ Vật qua thấu kính phân kì luông cho ảnh ảo nhỏ hơn vật
\( \to \left\{ \begin{array}{l}{A_1}{B_1} < AB\\{A_2}{B_2} > AB\end{array} \right. \to {A_2}{B_2} > {A_1}{B_1}\)
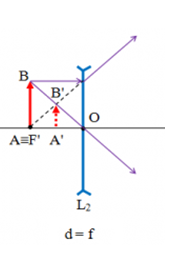
Vật \(AB\) đặt trước thấu kính phân kỳ có tiêu cự \(f\), có \(A\) nằm trên trục chính và cách thấu kính một khoảng \(OA\) cho ảnh \(A'B'\) cao bằng nửa vật \(AB\) khi:
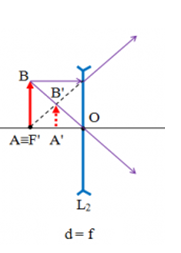
Vật \(AB\) đặt trước thấu kính phân kỳ có tiêu cự \(f\), có \(A\) nằm trên trục chính và cách thấu kính một khoảng \(OA\) cho ảnh \(A'B'\) cao bằng nửa vật \(AB\) khi \(OA = OF' = f\)
Một vật sáng được đặt tại tiêu điểm của thấu kính phân kỳ. Khoảng cách giữa ảnh và thấu kính là:
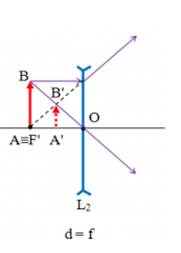
Ta có: \(d' = \frac{f}{2}\)
Một người quan sát vật \(AB\) qua một thấu kính phân kì, đặt cách mắt \(8cm\) thì thấy ảnh của mọi vật ở xa, gần đều hiện lên cách mắt trong khoảng \(64cm\) trở lại. Xác định tiêu cự của thấu kính phân kì:
Vì ảnh của tất cả các vật nằm trước thấu kính phân kì đều là ảnh ảo nằm trong khoảng từ tiêu điểm đến quang tâm của thấu kính, nên tiêu cự của thấu kính phân kì này là: \(64cm{\rm{ }} - {\rm{ }}8cm{\rm{ }} = {\rm{ }}56cm\)
Đặt ngón tay trước một thấu kính, rồi đặt mắt sau thấu kính ta thấy một ảnh lớn hơn chính ngón tay đó cùng chiều với ngón tay đó. Ảnh đó là ảnh thật hay ảnh ảo?. Thấu kính là hội tụ hay phân kì?
- Ta thấy thấu kính hội tụ cho:
+ ảnh ảo lớn hơn vật cùng chiều với vật
+ ảnh thật lớn hơn vật ngược chiều với vật
- Thấu kính phân kì luôn cho ảnh ảo nhỏ hơn vật
Theo dữ kiện bài toán thì ảnh lớn hơn vật và cùng chiều với vật nên thấu kính đó là thấu kính hội tụ và ảnh đó là ảnh ảo
Đặt vật \(AB\) trước một thấu kính phân kì có tiêu cự \(f = 12cm\). Vật \(AB\) cách thấu kính một khoảng \(d = 8cm\), \(A\) nằm trên trục chính. Biết vật \(AB = 6mm\)
Ảnh của vật \(AB\) cách thấu kính một đoạn bằng:
- Cách 1:
+ Ta có, ảnh của vật qua thấu kính phân kì
+ Từ hình, ta có:
- \(\Delta FB'O\) đồng dạng với \(\Delta IB'B\)
Ta suy ra: $\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}} = \frac{8}{{12}} = \frac{2}{3}$
- \(\Delta OAB\) đồng dạng với \(\Delta OA'B'\)
Ta suy ra:
\(\begin{array}{l}\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OB' + BB'}}{{OB'}} = 1 + \frac{{BB'}}{{OB'}} = 1 + \frac{2}{3} = \frac{5}{3}\\ \to OA' = \frac{3}{5}OA = \frac{3}{5}8 = 4,8cm\end{array}\)
- Cách 2: Sử dụng công thức thấu kính phân kì: \(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d}\)
Ta có: \(\left\{ \begin{array}{l}f = 12cm\\d = 8cm\\d' = ?\end{array} \right.\)
\(\frac{1}{f} = \frac{1}{{d'}} - \frac{1}{d} \to d' = \frac{{f{\rm{d}}}}{{f + d}} = \frac{{12.8}}{{12 + 8}} = 4,8cm\)
Đặt vật \(AB\) trước một thấu kính phân kì có tiêu cự \(f = 12cm\). Vật \(AB\) cách thấu kính một khoảng \(d = 8cm\), \(A\) nằm trên trục chính. Biết vật \(AB = 6mm\)
Ảnh của vật \(AB\) là \(A'B'\) có độ lớn bằng:
- Cách 1:
+ Từ hình, ta có:
- \(\Delta FB'O\) đồng dạng với \(\Delta IB'B\)
Ta suy ra: $\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}} = \frac{8}{{12}} = \frac{2}{3}$
- \(\Delta OAB\) đồng dạng với \(\Delta OA'B'\)
Ta suy ra:
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{OB}}{{OB'}} = \frac{{OB' + BB'}}{{OB'}} = 1 + \frac{2}{3} = \frac{5}{3}\\ \to A'B' = \frac{3}{5}AB = \frac{3}{5}.6 = 3,6mm\end{array}\)
- Cách 2: Sử dụng công thức tỉ lệ ảnh vật: \(\frac{h}{{h'}} = \frac{d}{{d'}}\)
Ta có: \(\left\{ \begin{array}{l}h = 6mm\\d = 8cm\\d' = 4,8cm\end{array} \right.\)
\( \to \frac{h}{{h'}} = \frac{d}{{d'}} \to h' = \frac{{d'}}{d}h = \frac{{4,8}}{8}.6 = 3,6mm\)
