Đặt vật \(AB\) trước một thấu kính phân kì có tiêu cự \(f = 12cm\). Vật \(AB\) cách thấu kính một khoảng \(d = 8cm\), \(A\) nằm trên trục chính. Biết vật \(AB = 6mm\)

Ảnh của vật \(AB\) là \(A'B'\) có độ lớn bằng:

- Cách 1:

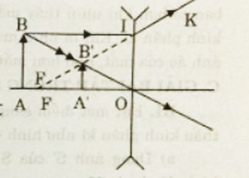
+ Từ hình, ta có:

• \(\Delta FB'O\) đồng dạng với \(\Delta IB'B\)

Ta suy ra: $\frac{{BI}}{{OF}} = \frac{{BB'}}{{OB'}} = \frac{8}{{12}} = \frac{2}{3}$

• \(\Delta OAB\) đồng dạng với \(\Delta OA'B'\)

Ta suy ra:

\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{OB}}{{OB'}} = \frac{{OB' + BB'}}{{OB'}} = 1 + \frac{2}{3} = \frac{5}{3}\\ \to A'B' = \frac{3}{5}AB = \frac{3}{5}.6 = 3,6mm\end{array}\)

- Cách 2:  Sử dụng công thức tỉ lệ ảnh vật: \(\frac{h}{{h'}} = \frac{d}{{d'}}\)

Ta có: \(\left\{ \begin{array}{l}h = 6mm\\d = 8cm\\d' = 4,8cm\end{array} \right.\)

\( \to \frac{h}{{h'}} = \frac{d}{{d'}} \to h' = \frac{{d'}}{d}h = \frac{{4,8}}{8}.6 = 3,6mm\)