I. Các kiến thức cần nhớ
1. Tam giác cân
Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
Ví dụ: ΔABC cân tại A ⇔AB=AC
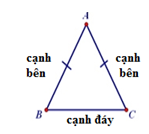
Tính chất:
Trong tam giác cân, hai góc ở đáy bằng nhau.
Ví dụ: ΔABC cân tại A ⇒ˆB=ˆC
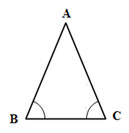
Dấu hiệu nhận biết
+ Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.
+ Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
2. Tam giác vuông cân
Định nghĩa: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.
Ví dụ: ΔABC vuông cân tại A ⇔{ˆA=900AB=AC
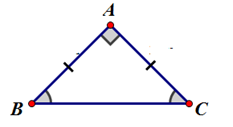
Tính chất
Mỗi góc nhọn của tam giác vuông cân bằng 450.
Ví dụ: ΔABC vuông cân tại A ⇒ˆB=ˆC=450.
3. Tam giác đều
Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.
Ví dụ: ΔABC đều ⇔AB=BC=CA
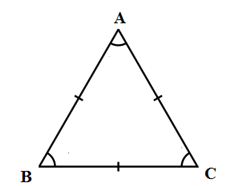
Tính chất
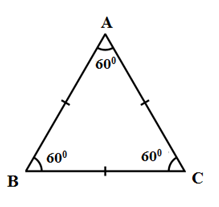
Trong tam giác đều, mỗi góc bằng 600.
Ví dụ: ΔABC đều ⇒ˆA=ˆB=ˆC=600.
Dấu hiệu nhận biết
+ Nếu tam giác có ba cạnh bằng nhau thì tam giác đó là tam giác đều
+ Nếu tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
+ Nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều.
II. Các dạng toán thường gặp
Dạng 1: Nhận biết một tam giác là tam giác cân, tam giác vuông cân, tam giác đều
Phương pháp:
Dựa vào dấu hiệu nhận biết tam giác cân, tam giác vuông cân, tam giác đều.
Dạng 2: Chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau. Tính độ dài đoạn thẳng, số đo góc
Phương pháp:
Sử dụng định nghĩa và tính chất của tam giác cân, tam giác vuông cân và tam giác đều.

