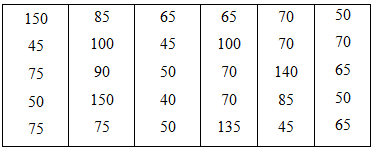
1. Dấu hiệu
Số liệu thống kê là các số liệu thu thập được khi điều tra về một dấu hiệu. Mỗi số liệu là một giá trị của dấu hiệu
Số tất cả các giá trị (không nhất thiết khác nhau) của dấu hiệu bằng số các đơn vị điều tra.
2. Tần số
Số lần xuất hiện của một giá trị trong dãy giá trị của dấu hiệu được gọi là tấn số của giá trị đó.
Chú ý:
Giá trị của dấu hiệu thường được kí hiệu là x và tần số của giá trị thường được kí hiệu là n.
n: là số các giá trị
x: là dấu hiệu.
3. Bảng tần số của dấu hiệu
* Từ bảng thu thập số liệu ban đầu ta có thể lập bảng tần số.
Bảng “tần số” thường được lập như sau:
+ Vẽ một khung hình chữ nhật gồm hai dòng
+ Dòng trên ghi các giá trị khác nhau của dáu hiệu theo thứ tự tăng dần
+ Dòng dưới ghi các tần số tương ứng với mỗi giá trị đó.
* Bảng tần số giúp người điều tra dễ có những nhận xét chung về sự phân phối các giá trị của dấu hiệu và tiện lợi cho việc tính toán sau này.
Ta cũng có thể lập bảng tần số theo hàng dọc.
4. Biểu đồ
* Biểu đồ đoạn thẳng:
+ Dựng hệ trục tọa độ, trục hoành biểu diễn các giá trị x, trục tung biểu diễn tần số n (độ dài đơn vị trên hai trục có thể khác nhau).
+ Xác định các điểm có tọa độ là cặp số gồm giá trị và tần số của nó (giá trị viết trước, tần số viết sau).
+ Nối mỗi điểm đó với điểm trên trục hoành có cùng hoành độ.
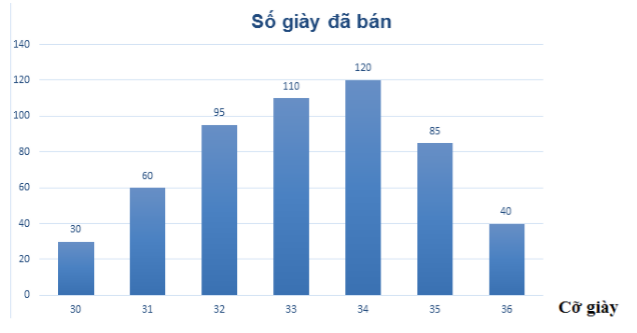
* Biểu đồ hình chữ nhật:
+ Các đoạn thẳng trong biểu đồ đoạn thẳng được thay bằng hình chữ nhật.
* Biểu đồ hình quạt:
+ Đó là một hình tròn được chia thành các hình quạt mà góc ở tâm của các hình quạt tỉ lệ với tần suất.
Chú ý: Tần suất f của một giá trị được tính theo công thức: f=nN trong đó N là số các giá trị, n là tần số của một giá trị , f là tần số của giá trị đó. Người ta thường biểu diễn tần suất dưới dạng phần trăm.
5. Số trung bình cộng
Dựa vào bảng “tần số”, ta có thể tính số trung bình cộng của một dấu hiệu (kí hiệu ¯X) như sau:
+ Nhân từng giá trị với tần số tương ứng;
+ Cộng tất cả các tích vừa tìm được;
+ Chia tổng đó cho số các giá trị (tức là tổng các tần số).
+ Công thức tính: ¯X=x1n1+x2n2+x3n3+...+xknkN
Trong đó:
x1,x2,...,xk là k giá trị khác nhau của dấu hiệu X.
n1,n2,...,nk là k tần số tương ứng.
N là số các giá trị.
Ý nghĩa của số trung bình cộng
+ Số trung bình cộng thường được dùng làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
+ Khi các giá trị của dấu hiệu có khoảng chênh lệch rất lớn đối với nhau thì không nên lấy số trung bình cộng làm “đại diện” cho dấu hiệu đó.
+ Số trung bình cộng có thể không thuộc dãy giá trị của dấu hiệu
6. Mốt của dấu hiệu
+ Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng “tần số”, kí hiệu là M0.
+ Có những dấu hiệu có hai mốt hoặc nhiều hơn.