Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^0},BC = 6cm.\) Đường vuông góc với \(AB\) tại \(A\) cắt \(BC\) ở \(D.\) Độ dài \(BD\) bằng:

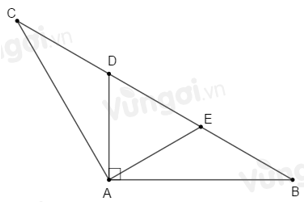
\(\Delta ABC\) cân tại \(\widehat A\) nên \(\widehat B = \widehat C = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{120}^o}}}{2} = {30^o}.\)

Ta có: \(\widehat {CAD} = \widehat {BAC} - \widehat {BAD} = {120^o} - {90^o} = {30^o}\)

\(\Delta ADC\) có: \(\widehat C = \widehat {CAD} = {30^o}\) nên \(\Delta ADC\) cân tại \(D\), suy ra \(DC = DA\)      (1)

Ta có: \(\widehat {ADB}\) là góc ngoài tại đỉnh \(D\) của \(\Delta ADC\) nên \(\widehat {ADB} = \widehat C + \widehat {CAD} = {30^o} + {30^o} = {60^o}.\)

Trên cạnh \(BD\) lấy \(E\) sao cho \(\widehat {BAE} = {30^o}\) thì \(E\) nằm giữa \(B\) và \(D.\)

\(\Delta AEB\) có: \(\widehat B = \widehat {BAE} = {30^o}\) nên \(\Delta AEB\) cân tại \(E\), suy ra \(AE = EB\)          (2)

Ta có: \(\widehat {DAE} = \widehat {BAD} - \widehat {BAE} = {90^o} - {30^o} = {60^o}.\)

\(\Delta ADE\) có: \(\widehat {DAE} = \widehat {ADE} = {60^o}\) nên \(\Delta ADE\) là tam giác đều, suy ra \(DA = DE = AE\)    (3)

Từ (1), (2) và (3) suy ra: \(DC = DE = EB = \dfrac{1}{3}BC.\)

Do đó \(BD = DE + EB = \dfrac{2}{3}BC = \dfrac{2}{3}.6 = 4\,\left( {cm} \right).\)