Câu hỏi:
2 năm trước
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có tâm $I$ thuộc đường thẳng \(\Delta :\dfrac{x}{1} = \dfrac{{y + 3}}{1} = \dfrac{z}{2}\) . Biết rằng mặt cầu $(S)$ có bán kính bằng \(2\sqrt 2 \) và cắt mặt phẳng $(Oxz)$ theo một đường tròn có bán kính $2$. Tìm tọa độ tâm $I$.
Trả lời bởi giáo viên
Đáp án đúng: a
Tâm $I$ thuộc đường thẳng $d$ nên $I\left( {t; - 3 + t;2t} \right)$
Phương trình mặt phẳng $\left( {{\rm{Oxz}}} \right):y = 0$
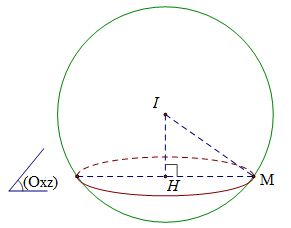
Ta có bán kính mặt cầu $IM = 2\sqrt 2 $, mặt cầu cắt mặt phẳng $(Oxz)$ theo đường tròn có bán kính $HM=2$ suy ra $d\left( {I,\left( {Oxz} \right)} \right) = IH = \sqrt {I{M^2} - H{M^2}} = \sqrt {8 - 4} = 2$
Ta có $\left| { - 3 + t} \right| = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 3 + t = 2}\\{ - 3 + t = - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 5 \Rightarrow I\left( {5;2;10} \right)}\\{t = 1 \Rightarrow I\left( {1; - 2;2} \right)}\end{array}} \right.$
Hướng dẫn giải:
+ Gọi tọa độ tâm theo tham số của đường thẳng.
+ Tìm tọa độ \(I\) dựa vào khoảng cách từ \(I\) đến mặt phẳng \(\left( {Oxz} \right)\).
