Trong hình vẽ, xe \(A\) kéo xe \(B\) bằng một sợi dây dài \(39\,m\) qua một ròng rọc ở độ cao \(12m\). Xe \(A\) xuất phát từ \(N\) và chạy với vận tốc không đổi \(2m/s\) theo chiều mũi tên.

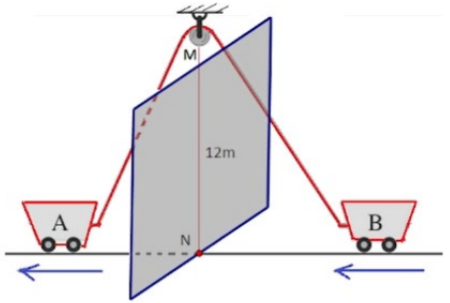
Tính vận tốc của xe \(B\) khi xe \(A\) cách \(N\) một khoảng là \(5m\).

Bước 1: Tìm mối quan hệ giữa x và t

Khi A sang trái thì x tăng dần và y giảm dần

Tạo mối quan hệ giữa y và t

Vì xe A chuyển động đều với vận tốc là 2m/s nên mối quan hệ giữa x và t là: \(x = v.t = 2t\)

Bước 2: Tìm mối quan hệ giữa y và t

Mà ta có \(\sqrt {{x^2} + 144}  + \sqrt {{y^2} + 144}  = 39\) nên:

\(\sqrt {4{t^2} + 144}  + \sqrt {{y^2} + 144}  = 39\)

\( \Leftrightarrow \sqrt {{y^2} + 144}  = 39 - 2\sqrt {{t^2} + 36} \)

\( \Leftrightarrow {y^2} + 144\)\( = {39^2} + 4\left( {{t^2} + 36} \right)\)\( - 4.39\sqrt {{t^2} + 36} \)

\(\begin{array}{l} \Leftrightarrow {y^2} = 4{t^2} + {39^2} - 156\sqrt {{t^2} + 36} \\y = \sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} \end{array}\)

Quãng đường A đi được là 5m nên ta có t=2,5(s)

Bước 3: Tính quãng đường tại t=2,5(s)

Vận tốc tại thời điểm t=2,5 của B là \(y'\left( {2,5} \right)\). Khi đó

\(\begin{array}{l}y' = \dfrac{{\left( {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} \right)'}}{{2\sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\\ = \dfrac{{8t - 156.\dfrac{t}{{\sqrt {{t^2} + 36} }}}}{{2\sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\\ = \dfrac{{4t\left( {2 - 39.\dfrac{t}{{\sqrt {{t^2} + 36} }}} \right)}}{{2\sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\\ = \dfrac{{2t\left( {2\sqrt {{t^2} + 36}  - 39t} \right)}}{{\sqrt {{t^2} + 36} \sqrt {4{t^2} - 156\sqrt {{t^2} + 36}  + {{39}^2}} }}\end{array}\)

Vậy \(y'\left( {2,5} \right) \approx  - 0,867\)

Vận tốc tức thời của xe B tại thời điểm xe A cách N 5m là -0,867(m/s).